Algebraic Identities

Algebraic Identities

An identity is an equality that remains true regardless of the values chosen for its variables.

We have already learnt about the following identities:

1. (a + b )² ≡ a ² + 2ab +b²

2. (a − b )² ≡ a ² − 2ab +b²

3. (a + b )(a −b) ≡ a ² −b²

4. (x + a )(x +b) ≡ x ² +(a + b )x +ab

Note

(i) a² + b² = (a +b)² −2ab

(ii) a² + b² = (a − b )² + 2ab

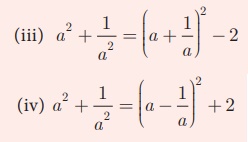
Example 3.16

Expand the following using identities: (i) (3x + 4y)² (ii) (2a − 3b)² (iii) (5x + 4y)(5x − 4y) (iv) (m + 5)(m − 8)

Solution

 (i) (3x +  4y)²           [we have (a + b)²  = a² + 2ab + b² ]

 (3x + 4y)² = (3x)² + 2(3x)(4y) +(4y)²  [put [a = 3x,  b = 4y]

 = 9x² + 24xy +16y²

(ii) (2a − 3b)²

[ we have (a − b)² = a² + 2ab + b² ]

(2a − 3b)² = (2a)² −2(2a)(3b) +(3b)²    put [a = 2a, b = 3b]

= 4a ² −12ab + 9b²

(iii) (5x + 4y)(5x − 4y)

[ we have (a + b)(a −b) = a² –b²]

 (5x + 4y)(5x − 4y) = (5x)² −(4y)² put [a = 5x b = 4y]

 = 25x² −16y²

 (iv) (m + 5) (m − 8)

[we have (x + a)(x-b) = x² + (a-b)x-ab]

(m + 5) (m − 8) = m² +(5 − 8)m −(5)(8)   put [x = m, a = 5, b = 8]

 = m² − 3m – 40

1. Expansion of Trinomial (a + b +c)²

We know that (x + y)² = x ² + 2xy + y²

Put x = a +b, y = c

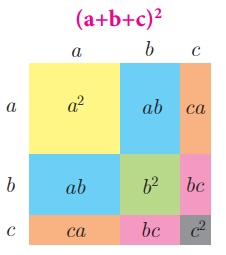
Then, (a + b +c)² = (a +b )² + 2(a +b)(c ) +c²

= a ² + 2ab + b² + 2ac + 2bc +c²

= a² +b² + c ² + 2ab + 2bc + 2ca

Thus, (a + b +c )² ≡ a ² +b ² + c ² + 2ab + 2bc + 2ca

Example 3.17

Expand (a − b +c)²

Solution

Replacing ‘b’ by ‘-b ’ in the expansion of

(a + b +c)² = a ² +b² + c ² + 2ab + 2bc + 2ca

(a + (−b) +c)² = a ² +(−b )² +c ² + 2a(−b ) + 2(−b)c + 2ca

= a ² +b² + c ² −2ab − 2bc + 2ca

Progress Check

Expand the following and verify :

(a + b + c)² = (−a − b −c)²

(−a +b +c)² = (a −b −c)²

(a − b +c)² = (−a + b −c)²

(a + b −c)² = (−a − b +c)²

Example 3.18

Expand (2x + 3y + 4z)²

Solution

We know that,

(a + b +c )² = a ² +b ² + c ² + 2ab + 2bc + 2ca

Substituting, a = 2x , b = 3y andc = 4z

(2x + 3y + 4z)² = (2x )² +(3y)² + (4z )² + 2(2x )(3y ) + 2(3y)(4z ) + 2(4z )(2x)

 = 4x ² + 9y² + 16z ² +12xy + 24yz +16xz

Example 3.19

Find the area of square whose side length is 3m + 2n − 4l

Solution

Area of square = side × side

= (3m + 2n − 4l)×(3m + 2n − 4l)

= (3m + 2n − 4l)²

We know that, (a + b +c)² = a² + b ² +c² + 2ab + 2bc + 2ca

[ 3m + 2n + (−4l)]² = (3m)² +(2n)² + (−4l)² + 2(3m)(2n) + 2(2n)(− 4l ) + 2(−4l)(3m)

 = 9m² + 4n² + 16l² +12mn − 16ln −24lm

Therefore, Area of square = [9m² + 4n² + 16l² +12mn − 16ln −24lm] sq.units.

Substituting

a = 3m,

b = 2n

c = –4l

2. Identities involving Product of Three Binomials

( x+ a )(x +b)(x +c) = [(x +a) (x + b )] (x +c)

= [x ² + (a +b)x +ab](x +c)

= x ² (x) +(a + b )(x)(x) +abx + x ²c +(a + b )(x)c +abc

= x ³ +ax ² + bx ² +abx + cx² +acx + bcx +abc

= x ³ +(a + b +c)x ² +(ab + bc +ca)x +abc

Thus, (x + a )(x +b)(x + c ) ≡ x ³ + (a +b + c )x ² +(ab +bc + ca)x +abc

Example 3.20

Expand the following:

(i) (x + 5)(x + 6)(x + 4) (ii ) (3x − 1)(3x + 2)(3x − 4)

Solution

We know that (x + a )(x +b)(x +c) = x ³ +(a + b +c)x ² + (ab +bc + ca)x +abc --(1)

(i) (x + 5)(x + 6)(x + 4)

Replace: a by 5, b by 6, c by 4 in (1)

= x ³ +(5 + 6 + 4)x² + (30 + 24 + 20)x +(5)(6)(4)

= x ³ +15x² + 74x +120

(ii) (3x − 1)(3x + 2)(3x − 4)

Replace :  x by 3x, a by –1,  b by 2, c by –4 in (1)

= (3x)³ +(− 1 + 2 − 4)(3x)² +(−2 − 8 + 4)(3x) + (−1)(2)(−4)

 = 27x³ +(− 3)9x² +(− 6)(3x) + 8

 = 27x³ −27x² − 18x + 8

3. Expansion of (x +y)³ and (x -y)³

(x + a )(x +b)(x +c) ≡ x ³ +(a + b +c)x² + (ab +bc + ca )x +abc

substituting a = b = c = y in the identity

we get, (x + y )(x + y )(x + y) = x³ +(y + y +y)x² + (yy +yy + yy )x + yyy

= x ³ + (3y)x ² + (3y² )x +y³

Thus, (x + y)³ ≡ x³ + 3x²y + 3xy² +y³ (or) (x + y)³ ≡ x³ +y³ + 3xy(x +y) by replacing y by -y, we get

(x − y )³ ≡ x³ − 3x²y + 3xy² −y³ (or) (x − y )³ ≡ x³ − y³ − 3xy(x −y)

Example 3.21

Expand (5a − 3b)³

Solution

We know that,

(x -y)³= x ³ − 3x²y + 3xy ² −y³

(5a − 3b)³ = (5a )³ − 3(5a)²(3b ) + 3(5a)(3b )² – (3b)³

= 125a ³ − 3(25a² )(3b ) + 3(5a)(9b ² ) – (3b)³

= 125a ³ −225a²b + 135ab ² −27b³

The following identity is also used:

 x ³ + y ³ + z ³ − 3xyz ≡ (x + y + z )(x² + y² + z² − xy −yz −zx)

We can check this by performing the multiplication on the right hand side.

Note

(i) If (x + y + z) = 0 then x ³ + y ³ + z ³ = 3xyz

Some identities involving sum, difference and product are stated without proof

(i) x³ + y³ ≡ (x + y )³ − 3xy(x + y) (ii) x³ − y³ ≡ (x − y )³ + 3xy(x −y)

Example 3.22

Find the product of (2x + 3y + 4z )(4x² + 9y ² +16z ² − 6xy −12yz − 8zx)

Solution

We know that, (a + b +c )(a² + b ² +c² − ab −bc −ca) = a ³ +b³ + c ³ − 3abc

(2x + 3y + 4z )(4x ² + 9y ² +16z ² − 6xy −12yz − 8zx)

= (2x )³ +(3y)³ + (4z )³ − 3(2x )(3y )(4z)

= 8x ³ + 27y ³ + 64z ³ −72xyz

Example 3.23

Evaluate 10³ − 15³ + 5³

Solution

We know that, if a + b +c = 0 , then a ³ + b ³ +c³ = 3abc

Here, a + b +c =10−15+5 = 0

Therefore, 10³ + (−15)³ + 5³ = 3(10)(−15)(5)

10³ −15³ +5³ = −2250

Replace a by 10, b by –15, c by 5