Linear Equation in Two Variables

Linear Equation in Two Variables

A linear equation in two variables is of the form ax + by + c = 0 where a, b and c are real numbers, both a and b are not zero (The two variables are denoted here by x and y and c is a constant).

Examples

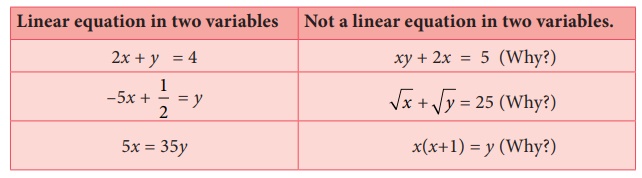
If an equation has two variables each of which is in first degree such that the variables are not multiplied with each other, then it is a linear equation in two variables (If the degree of an equation in two variables is 1, then it is called a linear equation in two variables).

An understanding of linear equation in two variables will be easy if it is done along with a geometrical visualization (through graphs). We will make use of this resource.

Why do we classify, for example, the equation 2x + y = 4 is a linear equation? You are right; because its graph will be a line. Shall we check it up?

We try to draw its graph. To draw the graph of 2x + y = 4, we need some points on the line so that we can join them. (These are the ordered pairs satisfying the equation).

To prepare table giving ordered pairs for 2x + y = 4. It is better, to take it as y = 4 – 2x. (Why? How?)

When x = –4, y = 4 – 2(–4) = 4 + 8 = 12

When x = –2,, y = 4 – 2(–2) = 4 + 4 = 8

When x = 0, y = 4 –2(0) = 4+0 = 4

When x = +1, y = 4 – 2(+1) = 4 – 2 = 2

When x = +3, y = 4 – 2(+3) = 4 – 6 = −2

Thus the values are tabulated as follows:

(To fix a line, do we need so many points? It is enough if we have two and probably one more for verification.)

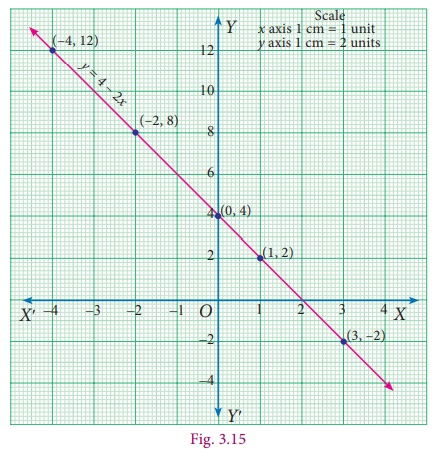
When you plot the points (−4,12), (−2,8), (0,4), (1,2) and (3,−2), you find that they all lie on a line.

This clearly shows that the equation 2x + y = 4 represents a line (and hence said to be linear).

All the points on the line satisfy this equation and hence the ordered pairs of all the points on the line are the solutions of the equation.

Example 3.42

Draw the graph for the following:

(i) y = 3x −1

(ii) y = (2/3)x + 3

Solution

(i) Let us prepare a table to find the ordered pairs of points for the line y = 3x −1.

We shall assume any value for x, for our convenience let us take −1, 0 and 1.

When x = −1, y = 3(–1)–1 = –4

When x = 0 , y = 3(0)–1 = –1

When x = 1 , y = 3(1)–1 = 2

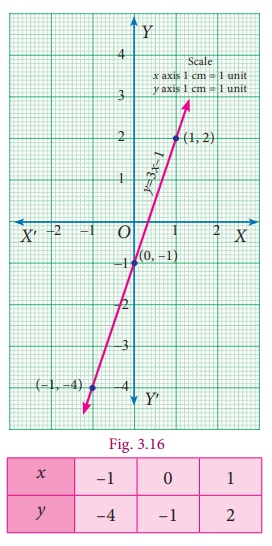
The points (x,y) to be plotted :

(−1, −4), (0, −1) and (1, 2).

(ii) Let us prepare a table to find the ordered pairs of points

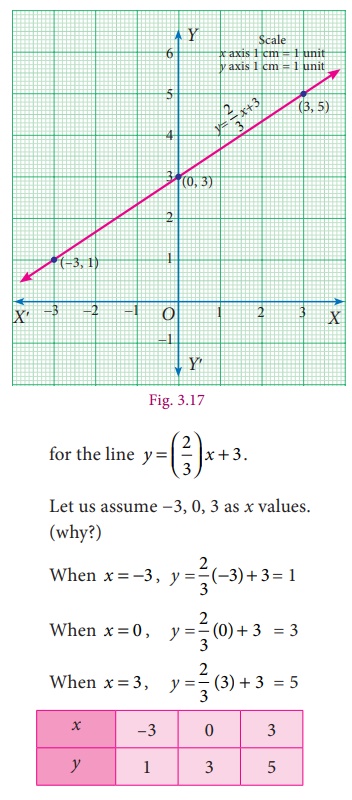
The points (x,y) to be plotted :

(−3,1), (0,3) and (3,5).