Factorising the Quadratic Polynomial (Trinomial)

Factorising the Quadratic Polynomial (Trinomial) of the type ax² + bx +c, a ≠ 0

The linear factors of ax² + bx +c will be in the form (kx + m) and (lx + n)

Thus, ax² + bx +c = (kx +m )(lx +n) = klx² +(lm + kn )x +mn

Comparing coefficients of x², x and constant term c on both sides.

We have, a = kl , b = (lm +kn) and c = mn, where ac is the product of kl and mn that is, equal to the product of lm and kn which are the coefficient of x. Therefore (kl × mn) = (lm ×kn) .

Steps to be followed to factorise ax² + bx +c :

Step 1 : Multiply the coefficient of x² and constant term, that is ac .

Step 2 : Split ac into two numbers whose sum and product is equal to b and ac respectively.

Step 3 : The terms are grouped into two pairs and factorise.

Example 3.27

Factorise 2x² + 15x + 27

Solution

Compare with ax² + bx +c

we get, a = 2, b = 15, c = 27

product ac = 2 ×27 = 54 and sum b = 15

We find the pair 6, 9 only satisfies “b = 15” and also “ac = 54”.

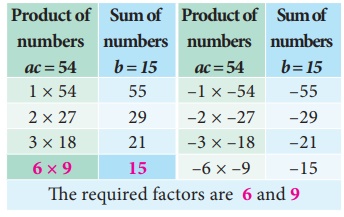
 we split the middle term as 6x and 9x

2x ² + 15x + 27 = 2x ² + 6x + 9x + 27

= 2x (x + 3) + 9(x + 3)

= (x + 3)(2x + 9)

Therefore, (x + 3) and (2x + 9) are the factors of 2x ² + 15x + 27 .

Example 3.28

Factorise 2x² − 15x + 27

Solution

Compare with ax ² + bx +c

a = 2, b = − 15, c = 27

product ac = 2×27 = 54, sum b=–15

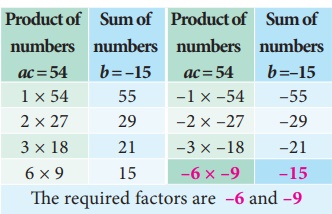
we split the middle term as –6x and –9x

2x² − 15x + 27 = 2x² −6x − 9x + 27

= 2x(x − 3) − 9(x − 3)

= (x − 3)(2x −9)

Therefore, (x − 3) and (2x − 9) are the factors of 2x² − 15x + 27.

Example 3.29

Factorise 2x² + 15x −27

Solution

Compare with ax ² + bx +c

Here, a = 2, b = 15, c = −27

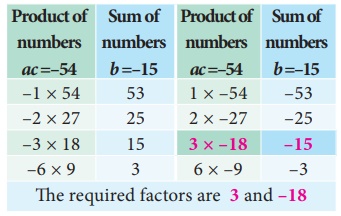
product ac = 2×–27 = –54, sum b=15

we split the middle term as 18x and –3x

2x² + 15x −27 = 2x² +18x − 3x −27

= 2x(x + 9) − 3(x + 9)

= (x + 9)(2x − 3)

Therefore, (x + 9) and (2x − 3) are the factors of 2x² + 15x −27.

Example 3.30

Factorise 2x² − 15x -27

Solution

Compare with ax ² + bx +c

Here,a = 2, b = − 15, c = −27

product ac = 2×–27=–54, sum b=–15

we split the middle term as –18x and 3x

2x ² − 15x -27 = 2x ² −18x + 3x −27

= 2x (x −9) + 3(x −9)

= (x −9)(2x + 3)

Therefore, (x − 9) and (2x + 3) are the factors of 2x² − 15x -27

Example 3.31

Factorise (x + y )² + 9(x + y ) + 20

Solution

Let x + y = p , we get p² + 9p + 20

Compare with ax² + bx +c,

We get a = 1, b = 9, c = 20

product ac = 1×20 = 20, sum b=9

 we split the middle term as 4p and 5p

p² + 9 p + 20 = p² + 4p + 5 p + 20

= p(p + 4) + 5(p + 4)

= ( p + 4)(p + 5)

Put, p = x +y we get, (x + y )² + 9(x + y ) + 20 = (x +y + 4)(x +y + 5)