Types of Matrices

Types of Matrices

In this section, we shall define certain types of matrices.

1. Row Matrix

A matrix is said to be a row matrix if it has only one row and any number of columns.

A row matrix is also called as a row vector.

For example, A = (8 9 4 3), B = (-√3/2 1 √3) 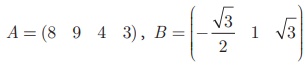 are row matrices of order 1×4 and 1×3 respectively. 

In general A = (a₁₁ a₁₂ a₁₃  … a_1n) is a row matrix of order 1×n.

2. Column Matrix

A matrix is said to be a column matrix if it has only one column and any number of rows. It is also called as a column vector.

For example,  are column matrices of order 3 ×1, 2 ×1 and 4 ×1 respectively.

In general,  is a column matrix of order m × 1.

3. Square Matrix

A matrix in which the number of rows is equal to the number of columns is called a square matrix. Thus a matrix A = (a_ij )_{m ×n} will be a square matrix if m = n

For example, 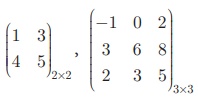 are square matrices.

In general, 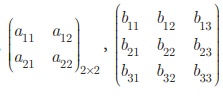 are square matrices of orders 2 × 2 and 3 × 3 respectively.

A = (a_ij )_{m ×m} is a square matrix of order m.

Definition : In a square matrix, the elements of the form a₁₁, a₂₂, a₃₃, . . . (i.e) a_ii are called leading diagonal elements. For example in the matrix 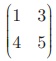, 1 and 5 are leading diagonal elements.

4. Diagonal Matrix

A square matrix, all of whose elements, except those in the leading diagonal are zero is called a diagonal matrix.

(ie) A square matrix A = (a_ij ) is said to be diagonal matrix if a_ij  = 0 for i ≠ j . Note that some elements of the leading diagonal may be zero but not all.

For example,  are diagonal matrices.

5. Scalar Matrix

A diagonal matrix in which all the leading diagonal elements are equal is called a scalar matrix.

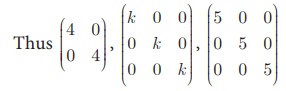
In general, A = (a_ij )_{m ×m} is said to be a scalar matrix if

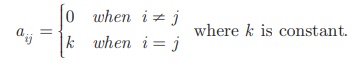
6. Identity (or) Unit Matrix

A square matrix in which elements in the leading diagonal are all “1” and rest are all zero is called an identity matrix (or) unit matrix.

Thus, the square matrix A = (a_ij) is an identity matrix if a_ij =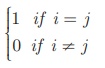 

A unit matrix of order n is written as I_n.

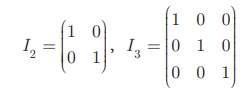 are identity matrices of order 2 and 3 respectively.

7. Zero matrix (or) null matrix

A matrix is said to be a zero matrix or null matrix if all its elements are zero.

For example, 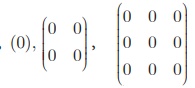 are all zero matrices of order 1×1, 2 × 2 and  3 × 3 but of different orders. We denote zero matrix of order n ×n by O_n.

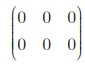 is a zero matrix of the order 2×3.

8. Transpose of a matrix

The matrix which is obtained by interchanging the elements in rows and columns of the given matrix A is called transpose of A and is denoted by A^T (read as A transpose). For example,

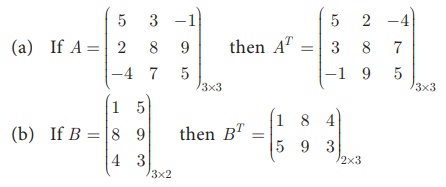
If order of A is m ×n then order of A^T  is n ×m . 

We note that (A^T )^T = A.

9. Triangular Matrix 

A square matrix in which all the entries above the leading diagonal are zero is called a lower triangular matrix.

If all the entries below the leading diagonal are zero, then it is called an upper triangular matrix.

Definition: 

A square matrix A = (a_ij )_{n ×n} is called upper triangular matrix if a_ij = 0 for = 0 for i > j and is called lower triangular matrix if a_ij  = 0 , i < j .

For example, A =  is an upper triangular matrix and B = 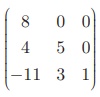 is a  lower triangular matrix.

Equal Matrices

Two matrices A and B are said to be equal if and only if they have the same order and each element of matrix A is equal to the corresponding element of matrix B. That is, a _ij = b_ij for all i, j.

For example, if 

then we note that A and B have same order and a_ij = b_ij for every i, j. Hence A and B are equal matrices.

Progress Check

1. The number of column(s) in a column matrix are _______.

2. The number of row(s) in a row matrix are _______.

3. The non-diagonal elements in any unit matrix are______.

4. Does there exist a square matrix with 32 elements?

The negative of a matrix

The negative of a matrix A_{m ×n} denoted by −A_{m ×n} is the matrix formed by replacing each element in the matrix A_{m ×n} with its additive inverse.

Additive inverse of an element k is -k . That is, every element of –A is the negative of the corresponding element of A.

For example, if 

Example 3.53

Consider the following information regarding the number of men and women workers in three factories I, II and III.

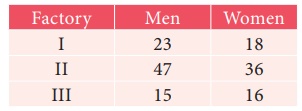
Represent the above information in the form of a matrix. What does the entry in the second row and first column represent?

Solution

The information is represented in the form of a 3 ×2 matrix as follows

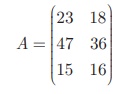
The entry in the second row and first column represent that there are 47 men workers in factory II

Example 3.54

If a matrix has 16 elements, what are the possible orders it can have?

Solution

We know that a matrix of order m ×n , has mn elements. Thus to find all possible orders of a matrix with 16 elements, we will find all ordered pairs of natural numbers whose product is 16.

Such ordered pairs are (1,16), (16,1), (4,4), (8,2), (2,8)

Hence possible orders are 1 × 16, 16 ×1 , 4 ×4 , 2 ×8 , 8 ×2

Example 3.55

Construct a 3 ×3 matrix whose elements are a _ij = i² j ²

Solution

The general 3×3 matrix is given by

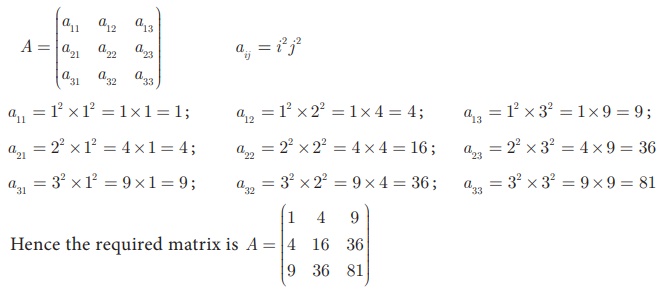
Example 3.56

Find the value of a, b, c, d from the equation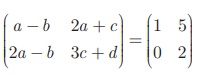 

Solution

The given matrices are equal. Thus all corresponding elements are equal.

Therefore,

 a − b = 1…(1)

2a + c = 5…(2)

2a − b = 0…(3)

3c + d = 2…(4)

(3) Gives 

2a − b = 0

2a = b …(5)

Put 2a = b in equation (1), a − 2a = 1 gives a = −1

Put a = −1 in equation (5), 2(− 1) = b gives b = −2

Put a = −1 in equation (2), 2(− 1) +c = 5   gives c = 7

Put c = 7 in equation (4),   3(7) + d = 2 gives d = −19

Therefore, a = −1, b = −2, c = 7, d = −19