Definition, Reduction, Example, Solution | Algebra - Rational Expressions | 10th Mathematics : UNIT 3 : Algebra
Chapter: 10th Mathematics : UNIT 3 : Algebra
Rational Expressions
Rational
Expressions
Definition :
An expression is called
a rational expression if it can be written in the form p(x) / q(x)
where p(x) and q(x) are polynomials and q(x)
≠ 0 . A rational expression is the ratio q (x)
of two polynomials.
The following are
examples of rational expressions.
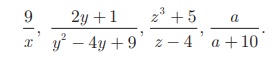
The rational expressions
are applied for describing distance-time, modeling multi-task problems, to
combine workers or machines to complete a job schedule and much more.
1. Reduction of Rational Expression
A rational expression p(x)
/ q(x) is said to be in its lowest form if GCD ( p(x
), q(x)) = 1.
To reduce a rational
expression to its lowest form, follow the given steps
(i) Factorize the
numerator and the denominator
(ii) If there are common
factors in the numerator and denominator, cancel them.
(iii) The resulting
expression will be a rational expression in its lowest form.
Example 3.13
Reduce the rational
expressions to its lowest form
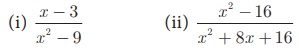
Solution
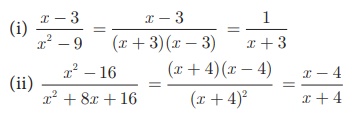
2. Excluded Value
A value that makes a
rational expression (in its lowest form) undefined is called an Excluded value.
To find excluded value
for a given rational expression in its lowest form, say p(x) / q(x), consider the denominator q(x)
= 0.
For example, the
rational expression 5/(x-10) is
undefined when x = 10 . So, 10 is called an excluded value for 5/(x-10)
Example 3.14
Find the excluded values
of the following expressions (if any).
(i) 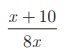
(ii) 
(iii) 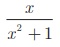
Solution
(i) 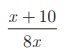
The expression 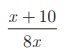 is undefined when 8x = 0 or x = 0 . Hence the excluded
value is 0.
is undefined when 8x = 0 or x = 0 . Hence the excluded
value is 0.
(ii) 
The expression  is undefined when 8p 2 + 13p + 5 = 0
is undefined when 8p 2 + 13p + 5 = 0
that is, (8p +
5)(p + 1) = 0
P= −5/8, p = −1 . The excluded values are -5/8
and -1.
(iii) 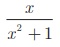
Here x2
≥ 0 for all x. Therefore , x2 + 1 ≥ 0 + 1 = 1, Hence, x 2 + 1 ≠ 0 for any x.
Therefore, Therefore, there can be no real excluded values for the given
rational expression x/(x2+1).
Related Topics