Properties of Multiplication of Matrix

Multiplication of Matrices

To multiply two matrices, the number of columns in the first matrix must be equal to the number of rows in the second matrix. Consider the multiplications of 3×3 and 3×2 matrices.

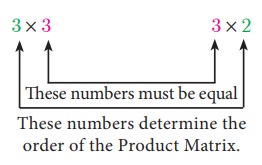
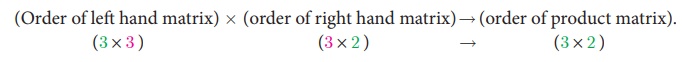
Matrices are multiplied by multiplying the elements in a row of the first matrix by the elements in a column of the second matrix, and adding the results

For example, product of matrices

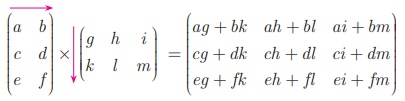
The product AB can be found if the number of columns of matrix A is equal to the number of rows of matrix B. If the order of matrix A is m ×n and B is n × p then the order of AB is m × p

Properties of Multiplication of Matrix

(a) Matrix multiplication is not commutative in general

If A is of order m ×n and B of the order n × p then AB is defined but BA is not defined. Even if AB and BA are both defined, it is not necessary that they are equal. In general AB ≠ BA.

(b) Matrix multiplication is distributive over matrix addition

(i) If  A,  B,  C  are  m ×n ,  n × p and  n × p matrices  respectively then A(B + C) = AB + AC (Right Distributive Property)

(ii) If  A,  B,  C  are  m ×n ,  m ×n and  n × p  matrices  respectively then(A + B)C = AC + BC (Left Distributive Property)

(c) Matrix multiplication is always associative

If A, B, C are m × n , n × p and p ×q matrices respectively then (AB)C = A(BC)

(d) Multiplication of a matrix by a unit matrix

If A is a square matrix of order n ×n and I is the unit matrix of same order then AI = IA = A .

Note

·           If x and y are two real numbers such that xy = 0 then either x = 0 or y = 0 . But this condition may not be true with respect to two matrices.

·           AB = 0 does not necessarily imply that A = 0 or B = 0 or both A, B = 0

Illustration

Example 3.64

If 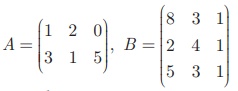, find AB. 

Solution

We observe that A is a 2 ×3 matrix and B is a 3×3 matrix, hence AB is defined and it will be of the order 2 × 3.

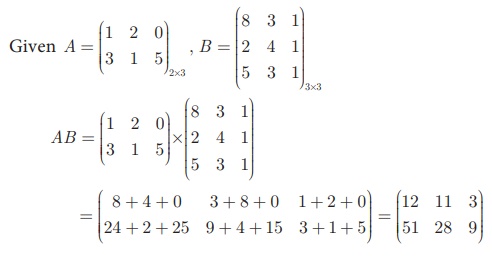
Example 3.65

If  find AB and BA. Check if AB = BA.

Solution

We observe that A is a 2 ×2 matrix and B is a 2 ×2 matrix, hence AB is defined and it will be of the order 2 ×2 .

Therefore, AB ≠ BA.

Example 3.66

Show that A and B satisfy commutative property with respect to matrix multiplication.

Solution

We have to show that AB = BA

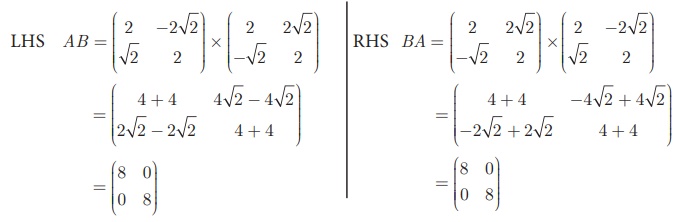
Hence LHS = RHS (ie) AB = BA

Example 3.67

Substituting y = 2 in (1), 2x + 2 = 4 gives x = 1

Therefore, x = 1 , y = 2 .

Note

·           If A and B are any two non zero matrices, then (A + B)²  ≠ A²  + 2AB + B^2.

·           However if AB = BA then  (A + B)²  = A²  + 2AB + B²

Example 3.68

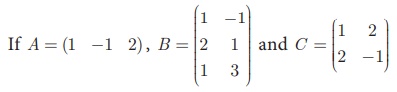
show that (AB)C = A(BC) .

Solution

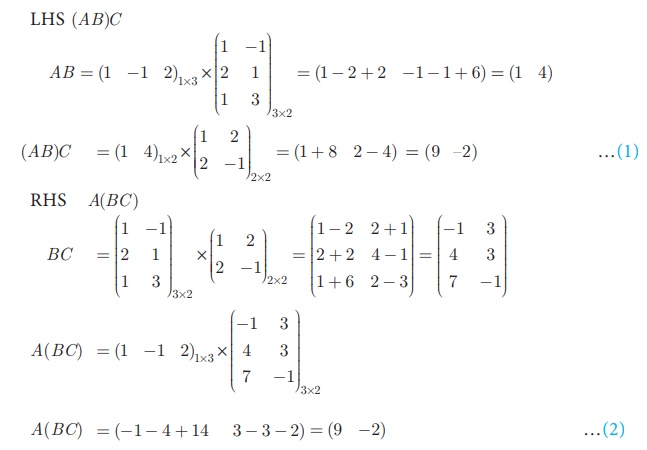
A(BC)  = (−1 − 4 + 14 3 − 3 − 2) =(9−2) …(2)

From (1) and (2), (AB)C = A(BC) .

Example 3.69

If 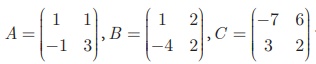 verify that A(B + C) = AB + AC.

Solution

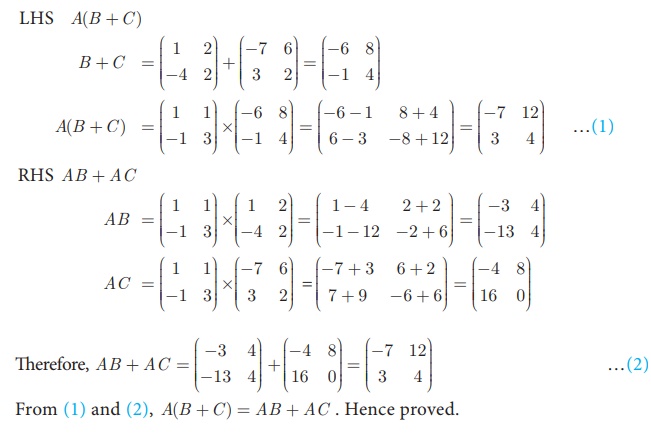
Example 3.70

If 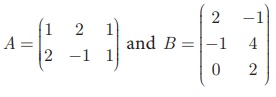 show that (AB)^T = B^TA^T

Solution

From (1) and (2),(AB)^T = B ^T A^T .

Hence proved.