Quadratic Equations

Quadratic Equations

Introduction

Arab mathematician Abraham bar Hiyya Ha-Nasi, often known by the Latin name Savasorda, is famed for his book ‘Liber Embadorum’ published in 1145 AD(CE) which is the first book published in Europe to give the complete solution of a quadratic equation.

For a period of more than three thousand years beginning from early civilizations to current times, humanity knew how to solve a general quadratic equation in terms of its co-efficients by using four arithmetical operations and extraction of roots. This process is called “Solving by Radicals”. Huge amount of research has been carried to this day in solving various types of equations.

Quadratic Expression

An expression of degree n in variable x is a₀xⁿ+ a₁xⁿ⁻¹+a₂xⁿ⁻²+ ... +a_n-1x +a_n where a₀ ≠0  and  a₁ , a₂,...a_n are real numbers. a ₀ , a₁, a ₂ , ... a_n are called coefficients of the expression.

In particular an expression of degree 2 is called a Quadratic Expression which is expressed as p(x) = ax ² +bx +c, a ≠0 and a, b, c are real numbers.

1. Zeroes of a Quadratic Polynomial

Let p(x) be a polynomial. x=a is called zero of p(x) if p(a) = 0

For example, if p(x) = x²–2x–8 then p(–2)=4+4–8 = 0 and p(4) = 16– 8 –8 = 0

Therefore –2 and 4 are zeros of the polynomial p(x) = x²–2x–8.

2. Roots of Quadratic Equations

Let ax² + bx +c = 0, (a ≠ 0) be a quadratic equation. The values of x such that the expression ax 2 + bx + c becomes zero are called roots of the quadratic equation ax ² + bx +c = 0 .

We have, ax ² + bx + c = 0

3. Formation of a Quadratic Equation

If a and b are roots of a quadratic equation ax² + bx +c = 0 then

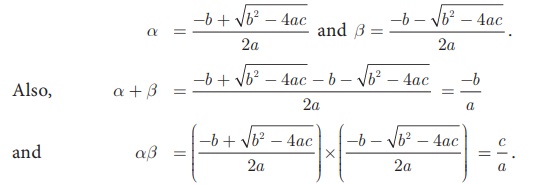
Since, (x - a) and (x - b) are factors of ax² + bx +c = 0 ,

We have (x - α)(x - β) = 0

Hence, x ² − (α + β)x + αβ = 0

That is, x² - (sum of roots) x  + product of roots = 0 is the general form of the quadratic equation when the roots are given.

Example 3.24

Find the zeroes of the quadratic expression x² + 8x + 12.

Solution

Let p(x)= x² + 8x + 12 =(x+2)(x+6)

p(–2)= 4 – 16 + 12=0

p(–6)= 36 – 48 + 12=0

Therefore –2 and –6 are zeros of p(x)= x² + 8x + 12

Example 3.25

Write down the quadratic equation in general form for which sum and product of the roots are given below.

(i) 9, 14

(ii) – 7/2 , 5/2

(iii) – 3/5 , - 1/2

Solution

(i) General form of the quadratic equation when the roots are given is x² - (sum of the roots ) x + product of the roots = 0

x ² − 9x + 14 = 0

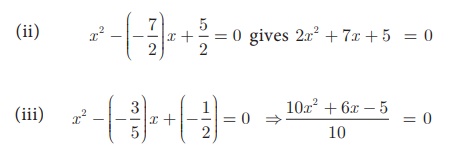
Therefore, 10x ² + 6x − 5 = 0.

Example 3.26

Find the sum and product of the roots for each of the following quadratic equations :

(i) x ² + 8x − 65 = 0

(ii) 2x² + 5x + 7 = 0

(iii) kx ² − k ² x − 2k ³  = 0

Solution 

Let a and b be the roots of the given quadratic equation

x ² + 8x − 65 = 0

a = 1,  b = 8,  c = –65

α + β = −b/a = –8 and αβ = c/a  = –65

α + β = −8 ;  αβ = −65

(ii) 2x ² + 5x + 7 = 0

a = 2,  b = 5,  c = 7

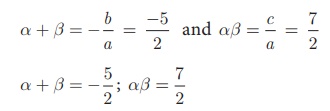
(iii) kx ² − k ² x − 2k ³  = 0

a = k,  b = -k² ,  c = –2k³