Example, Solution | Algebra - Solving a Quadratic Equation by Completing the Square Method | 10th Mathematics : UNIT 3 : Algebra
Chapter: 10th Mathematics : UNIT 3 : Algebra
Solving a Quadratic Equation by Completing the Square Method
Solving a Quadratic
Equation by Completing the Square Method
In deriving the formula
for the roots of a quadratic equation we used completing the squares method.
The same technique can be applied in solving any given quadratic equation
through the following steps
Step 1 Write the quadratic equation in
general form ax2 + bx +c = 0 .
Step 2 Divide both sides of the equation
by the coefficient of x2
if it is not 1.
Step 3 Shift the constant term to the
right hand side.
Step 4 Add the square of one-half of the
coefficient of x to both sides.
Step 5 Write the left hand side as a
square and simplify the right hand side.
Step 6 Take the square root on both sides and solve for x.
Example 3.31
Solve x2 − 3x − 2 = 0
Solution
x2 − 3x − 2 = 0
x2 - 3x = 2 (Shifting the
Constant to RHS)

Example 3.32
Solve 2x 2
− x −1 = 0
Solution 2x2 − x
−1 = 0
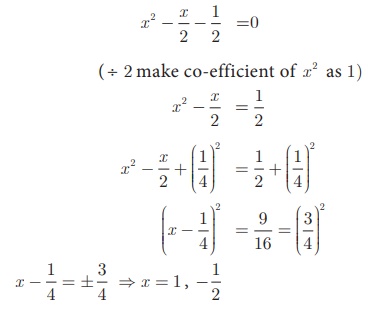
Related Topics