Solving Problems Involving Quadratic Equations

Solving Problems Involving Quadratic Equations

Steps to solve a problem

Step 1 Convert the word problem to a quadratic equation form

Step 2 Solve the quadratic equation obtained in any one of the above three methods.

Step 3 Relate the mathematical solution obtained to the statement asked in the question.

Example 3.37

The product of Kumaran’s age (in years) two years ago and his age four years from now is one more than twice his present age. What is his present age?

Solution

Let the present age of Kumaran be x years. 

Two years ago, his age = (x − 2)  years.

Four years from now, his age = (x + 4)  years.

Given,

(x − 2)(x + 4)  = 1 +2x

x² + 2x − 8 = 1 +2x gives (x − 3)(x + 3) = 0 then, x = ±3

Therefore, x = 3 (Rejecting −3 as age cannot be negative)

Kumaran’s present age is 3 years.

Example 3.38

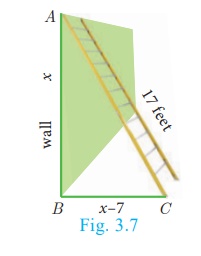
A ladder 17 feet long is leaning against a wall. If the ladder, vertical wall and the floor from the bottom of the wall to the ladder form a right triangle, find the height of the wall where the top of the ladder meets if the distance between bottom of the wall to bottom of the ladder is 7 feet less than the height of the wall?

Solution

Let the height of the wall AB = x feet

As per the given data BC = (x–7) feet

In the right triangle ABC, AC =17 ft, BC = (x–7) feet

By Pythagoras theorem, AC² = AB² + BC²

(17)²  = x²  + (x − 7)² ; 289 = x² + x² − 14x + 49

x² − 7x −120 = 0 hence,  (x − 15)(x + 8) = 0 then, x = 15 (or) −8

Therefore, height of the wall AB = 15 ft (Rejecting −8 as height cannot be negative)

Example 3.39

A flock of swans contained x² members. As the clouds gathered, 10x went to a lake and one-eighth of the members flew away to a garden. The remaining three pairs played about in the water. How many swans were there in total?

Solution

As given there are x² swans.

As per the given data x² − 10x – (1/8)x² = 6 we get, 7x² − 680x − 48 = 0

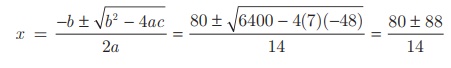
Therefore, x = 12, -4/7

Here x = 4/7 is not possible as the number of swans cannot be negative.

Hence, x = 12. Therefore total number of swans is x² = 144.

Example 3.40

A passenger train takes 1 hr more than an express train to travel a distance of 240 km from Chennai to Virudhachalam. The speed of passenger train is less than that of an express train by 20 km per hour. Find the average speed of both the trains.

Solution

Let the average speed of passenger train be x km/hr.

Then the average speed of express train will be (x + 20) km/hr

Time taken by the passenger train to cover distance of 240 km = 240/x hr

Time taken by express train to cover distance of 240 km = 240 / (x+20) hr

Given,

x ² + 20x – 4800 = 0 gives, (x + 80)(x − 60) = 0 we get, x = –80 or 60.

Therefore x = 60 (Rejecting -80 as speed cannot be negative)

Average speed of the passenger train is 60 km/hr

Average speed of the express train is 80 km/hr.