Chapter: 10th Mathematics : UNIT 3 : Algebra
Multiplication of Matrix by a Scalar
We can multiply the elements of the given matrix A by a non-zero number k to obtain a new matrix kA whose elements are multiplied by k. The matrix kA is called scalar multiplication of A.
Multiplication of Matrix by a Scalar
We can multiply the elements of the given matrix A by a non-zero number k to obtain a new matrix kA whose elements are multiplied by k. The matrix kA is called scalar multiplication of A.
Thus if A = (aij )m ×n then , kA = (kaij )m ×n for all i = 1,2,…,m and for all j = 1,2,…,n.
Example 3.60
If A = 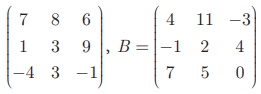 then Find 2A+B.
then Find 2A+B.
Solution
Since A and B have same order 3 ×3 , 2A + B is defined.
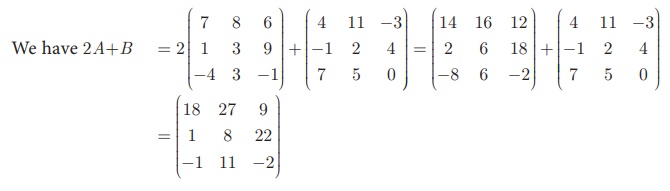
Example 3.61
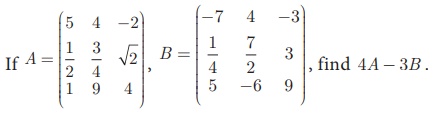
Solution
Since A, B are of the same order 3 ×3 , subtraction of 4A and 3B is defined.
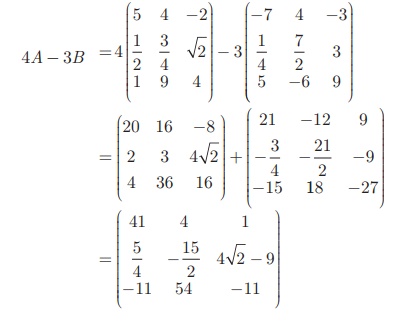
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
10th Mathematics : UNIT 3 : Algebra : Multiplication of Matrix by a Scalar |
Related Topics
10th Mathematics : UNIT 3 : Algebra