Finding the Square Root of a Polynomial by Division Method

Finding the Square Root of a Polynomial by Division Method

The long division method in finding the square root of a polynomial is useful when the degree of the polynomial is higher.

Example 3.21

Find the square root of 64x⁴ − 16x³ + 17x ² − 2x + 1

Solution

Note

Before proceeding to find the square root of a polynomial, one has to ensure that the degrees of the variables are in descending or ascending order.

Example 3.22 Find the square root of the expression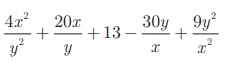 

Solution

Example 3.23

If 9x⁴ + 12x³ + 28x² + ax +b is a perfect square, find the values of a and b.

Solution

Because the given polynomial is a perfect square a − 16 = 0 , b − 16 = 0 Therefore a = 16 , b = 16 .