Operations of Rational Expressions

Operations of Rational Expressions

We have studied the concepts of addition, subtraction, multiplication and division of rational numbers in previous classes. Now let us generalize the above for rational expressions.

Multiplication of Rational Expressions

If 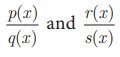 are two rational expressions where q (x) ≠ 0, s (x) ≠ 0 ,

their product is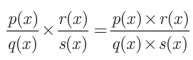 

In other words, the product of two rational expression is the product of their numerators divided by the product of their denominators and the resulting expression is then reduced to its lowest form.

Division of Rational Expressions

If 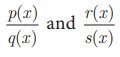 are two rational expressions, where q (x), s (x) ≠ 0 then,

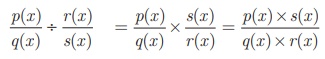
Thus division of one rational expression by other is equivalent to the product of first and reciprocal of the second expression. If the resulting expression is not in its lowest form then reduce to its lowest form.

Example 3.15

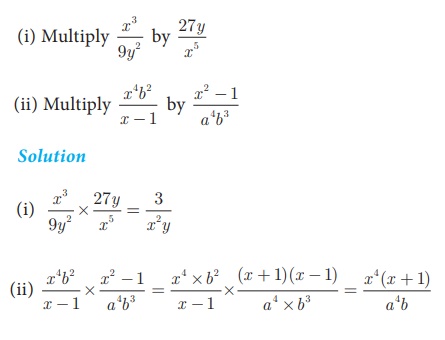
Example 3.16 Find 

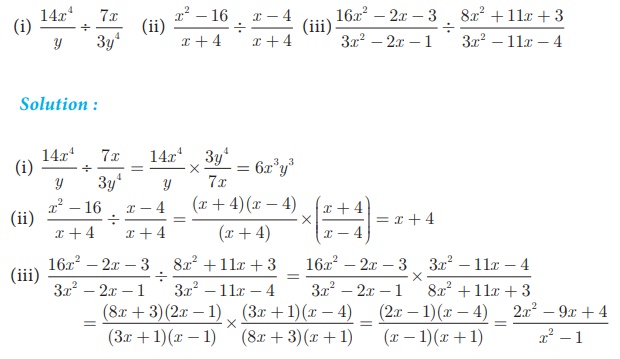
Addition and Subtraction of Rational Expressions

Addition and Subtraction of Rational Expressions with Like Denominators

(i) Add or Subtract the numerators

(ii) Write the sum or difference of the numerators found in step (i) over the common denominator.

(iii) Reduce the resulting rational expression into its lowest form.

Example 3.17 Find 

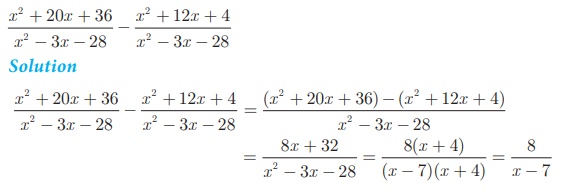
Addition and Subtraction of Rational Expressions with unlike Denominators

(i) Determine the Least Common Multiple of the denominator.

(ii) Rewrite each fraction as an equivalent fraction with the LCM obtained in step (i). This is done by multiplying both the numerators and denominator of each expression by any factors needed to obtain the LCM.

(iii) Follow the same steps given for doing addition or subtraction of the rational expression with like denominators.

Example 3.18 

Simplify