Example Solved Problem | Mathematics Algebra - Nature of Roots of a Quadratic Equation | 10th Mathematics : UNIT 3 : Algebra
Chapter: 10th Mathematics : UNIT 3 : Algebra
Nature of Roots of a Quadratic Equation
Nature of Roots of a Quadratic Equation
The roots of the quadratic equation ax2 + bx
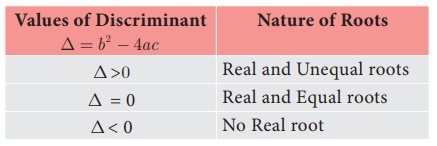
+c = 0 , a ≠ 0 are found using the formula x =  Here, b2 - 4ac called as the discriminant (which is denoted 2a
by Δ ) of the quadratic equation, decides the nature of roots as
follows
Here, b2 - 4ac called as the discriminant (which is denoted 2a
by Δ ) of the quadratic equation, decides the nature of roots as
follows
Example 3.41
Determine the nature of roots for the following quadratic
equations
(i) x2 − x − 20 = 0
(ii) 9x2 − 24x + 16 = 0
(iii) 2x2 − 2x + 9 = 0
Solution
(i) x2 − x − 20 = 0
Here, a = 1, b = −1 , c = −20
Now, Δ = b2 − 4ac
Δ = (− 1)2 −
4(1)(−20) = 81
Here, Δ = 81 > 0 . So,
the equation will have real and unequal roots
(ii) 9x2 − 24x + 16 = 0
Here, a = 9 , b = −24 , c =
16
Now, Δ = b2 − 4ac = (−24)2 − 4
(9 )(16)=0
Here,
∆ = 0 . So, the equation will have real and equal roots.
(iii) 2x2 − 2x + 9 = 0
Here, a = 2 , b = −2 , c =
9
Now, Δ = b2
− 4ac = (−2 )2 − 4(2 )(9 ) = −68
Here, Δ = − 68 < 0 . So, the equation will have no real roots.
Example 3.42
(i) Find the values of ‘k’, for which the quadratic
equation
kx 2 − (8k + 4) + 81 = 0
has real and equal roots?
(ii) Find the values of ‘k’ such that quadratic equation
(k + 9)x2 + (k + 1)x + 1 =
0 has no real roots?
Solution
(i) kx2 − (8k + 4) + 81 = 0
Since the equation has real and equal roots, Δ = 0.
That is, b2 − 4ac = 0
Here, a = k , b = −(8k + 4) , c
= 81
That is, [ −(8k + 4)]2 − 4(k )(81) =
0
64k2 + 64k + 16 − 324k = 0
64k2 − 260k + 16 = 0
dividing by 4 we get 16k2 − 65k + 4 = 0
(16k − 1)(k − 4) = 0 then, k = 1/16 or k
= 4
(ii) (k + 9)x2 + (k + 1)x +
1 = 0
Since the equation has no real roots, Δ < 0
That is, b2 − 4ac < 0
Here, a = k + 9 , b = k + 1 , c
= 1
That is, (k + 1)2 − 4(k + 9)(1) < 0
k 2 + 2k + 1 – 4k − 36 < 0
k 2 − 2k − 35 < 0
(k + 5)(k − 7) < 0
Therefore, − 5 < k < 7 . {If α
< β and if (x − α)(x − β) < 0 then, α
< x < β }.
Example 3.43
Prove that the equation x2 (p2 + q 2 ) + 2x(pr + qs) + r2 + s2 = 0 has no real roots. If ps = qr
, then show that the roots are real and equal.
Solution
The given quadratic equation is, x2 ( p2 + q2 ) + 2x ( pr + qs) + r2 + s2 = 0
Here,
a = p2 +q2 , b =
2(pr +qs) , c = r2 + s2
Now, Δ = b2 − 4ac = [2( pr + qs)]2 − 4( p2
+ q2 )( r 2 + s2 )
= 4 [p2r2
+ 2pqrs + q2s2 − q2r2
– p2s2 – q2r2 – q2s2
]
= 4 [–p2s2
+ 2pqrs − q2r2] = −4 [(ps − qr)2]
<0 ...(1)
since, Δ = b2 − 4ac
< 0 , the roots are not real.
If ps = qr then Δ = − 4[ps
– qr]2 = - 4[qr − qr]2 = 0 (using (1))
Thus, Δ = 0 if ps = qr and so
the roots will be real and equal.
Related Topics