Points to Remember

Points to Remember

·           A system of linear equations in three variables will be according to one of the following cases.

(i) Unique solution

(ii) Infinitely many solutions

(iii) No solution

·           The least common multiple of two or more algebraic expressions is the expression of lowest degree (or power) such that the expressions exactly divides it.

·           A polynomial of degree two in variable x is called a quadratic polynomial in x. Every quadratic polynomial can have atmost two zeroes. Also the zeroes of a quadratic polynomial intersects the x-axis

·           The  roots  of  the  quadratic equation  ax ² + bx +c = 0 ,  (a ≠ 0)  are  given  by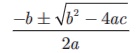 

·           For a quadratic equation ax ² + bx +c ≠ 0

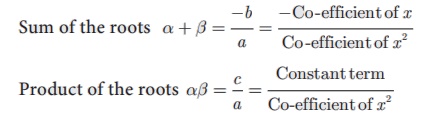
·           If the roots of a quadratic equation are α and β , then the equation is given by x ² − (α + β)x + αβ =0 .

·           The value of the discriminant ( Δ = b ² − 4ac) decides the nature of roots as follows

(i) When Δ > 0 , the roots are real and unequal.

(ii) When Δ = 0 , the roots are real and equal.

(iii) When Δ < 0 , there are no real roots.

·           Solving quadratic equation graphically.

·           A matrix is a rectangular array of elements arranged in rows and columns.

·           Order of a matrix

If a matrix A has m number of rows and n number of columns, then the order of the matrix A is (Number of rows)×(Number of columns) that is, m ×n .We read m ×n as m cross n or m by n. It may be noted that m ×n is not a product of m and n.

·           Types of matrices

(i) A matrix is said to be a row matrix if it has only one row and any number of columns. A row matrix is also called as a row vector.

(ii) A matrix is said to be a column matrix if it has only one column and any number of rows. It is also called as a column vector.

(iii) A matrix in which the number of rows is equal to the number of columns is called a square matrix.

(iv) A square matrix, all of whose elements, except those in the leading diagonal are zero is called a diagonal matrix.

(v) A diagonal matrix in which all the leading diagonal elements are same is called a scalar matrix.

(vi) A square matrix in which elements in the leading diagonal are all “1” and rest are all zero is called an identity matrix (or) unit matrix.

(vii) A matrix is said to be a zero matrix or null matrix if all its elements are zero.

(viii) If A is a matrix, the matrix obtained by interchanging the rows and columns of A is called its transpose and is denoted by AT .

(ix) A square matrix in which all the entries above the leading diagonal are zero is called a lower triangular matrix.

If all the entries below the leading diagonal are zero, then it is called an upper triangular matrix.

(x) Two matrices A and B are said to be equal if and only if they have the same order and each element of matrix A is equal to the corresponding element of matrix B. That is, a _ij = b_ij for all i, j.

·           The negative of a matrix A_{m ×n} denoted by −A_{m ×n} is the matrix formed by replacing each element in the matrix A_{m ×n} with its additive inverse.

·           Addition and subtraction of matrices

Two matrices can be added or subtracted if they have the same order. To add or subtract two matrices, simply add or subtract the corresponding elements.

·           Multiplication of matrix by a scalar

We can multiply the elements of the given matrix A by a non-zero number k to obtain a new matrix kA whose elements are multiplied by k. The matrix kA is called scalar multiplication of A.

Thus if A = (a_ij )_{m ×n} then , kA = (ka_ij )_{m ×n} for all i = 1,2,…,m and for all j = 1,2,…,n.