Greatest Common Divisor (GCD) or Highest Common Factor (HCF) of Polynomials

Greatest Common Divisor (GCD) or Highest Common Factor (HCF) of Polynomials

In our previous class we have learnt how to find the GCD (HCF) of second degree and third degree expressions by the method of factorization. Now we shall learn how to find the GCD of the given polynomials by the method of long division.

As discussed in Chapter 2, (Numbers and Sequences) to find GCD of two positive integers using Euclidean Algorithm, similar techniques can be employed for two given polynomials also.

The following procedure gives a systematic way of finding Greatest Common Divisor of two given polynomials f (x ) and g (x) .

Step 1 First, divide f(x) by g (x) to obtain f (x ) = g (x )q (x ) + r (x) whereq (x) is the quotient and r (x) is the remainder. Then, deg [r (x)] < deg [g (x )]

Step 2 If the remainder r (x) is non-zero, divide g (x) by r (x) to obtain g (x ) = r (x )q (x ) + r₁ (x ) where r₁ (x ) is the new remainder. Then deg [r₁ (x) ] < deg [r (x )] . If the remainder r₁ (x ) is zero, then r (x) is the required GCD.

Step 3 If r₁ (x ) is non-zero, then continue the process until we get zero as remainder. The divisor at this stage will be the required GCD.

We write GCD [f (x ), g(x)]  to denote the GCD of the polynomials f (x ), g (x ).

Note

If f (x ) and g (x) are two polynomials of same degree then the polynomial carrying the highest coefficient will be the dividend. In case, if both have the same coefficient then compare the next least degree’s coefficient and proceed with the division.

Progress Check

1. When two polynomials of same degree has to be divided, __________ should be considered to fix the dividend and divisor.

2. If r (x ) = 0 when f(x) is divided by g(x) then g(x) is called ________ of the polynomials.

3. If f (x ) = g (x )q (x ) + r (x), _________ must be added to f(x) to make f(x) completely divisible by g(x).

4. If f (x ) = g (x )q (x ) + r (x), _________ must be subtracted to f(x) to make f(x) completely divisible by g(x).

Example 3.10

Find the GCD of the polynomials x³ + x² − x + 2 and 2x³ − 5x² + 5x − 3 .

Solution

Let f (x ) = 2x ³ − 5x ²  + 5x – 3 and g (x) = x ³ + x ² − x + 2

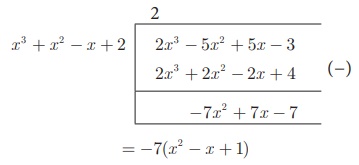
− 7(x ² − x + 1) ≠ 0 , note that -7 is not a divisor of g (x)

Now dividing g (x) = x³ + x² − x + 2 by the new remainder x² − x +1 (leaving the constant factor), we get

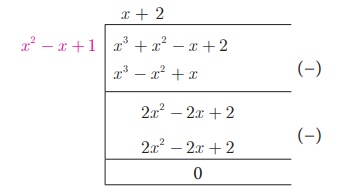
Here, we get zero remainder

Therefore, GCD(2x ³ − 5x ² + 5x − 3, x ³ + x ² − x + 2) = x ² − x + 1

Example 3.11

Find the GCD of 6x ³ − 30x ² + 60x − 48 and 3x ³ − 12x ² + 21x −18.

Solution

Let, f (x) = 6x ³ − 30x ² + 60x − 48 = 6(x ³ − 5x ² + 10x − 8) and g

(x) = 3x ³ − 12x ² + 21x − 18 = 3 (x ³ − 4x ² + 7x − 6)

Now, we shall find the GCD of x³ − 5x² + 10x − 8 and x³  − 4x² + 7x – 6

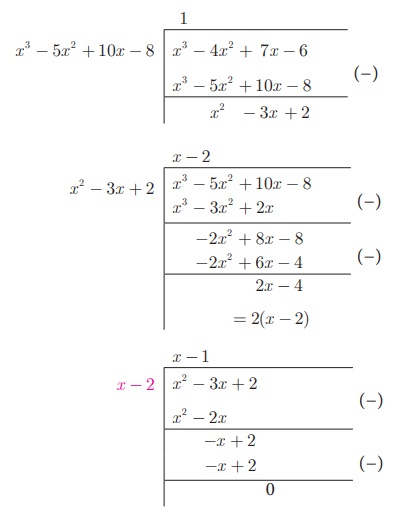
Here, we get zero as remainder.

GCD of leading coefficients 3 and 6 is 3.

Thus, GCD [(6x ³ − 30x ²  + 60x − 48, 3x ³ − 12x ²  + 21x − 18)] = 3(x −2) .