Example Solved Problem | Mathematics - The Relation between Roots and Coefficients of a Quadratic Equation | 10th Mathematics : UNIT 3 : Algebra
Chapter: 10th Mathematics : UNIT 3 : Algebra
The Relation between Roots and Coefficients of a Quadratic Equation
The Relation between Roots and Coefficients of
a Quadratic Equation
Let α and β are the roots of the equation ax2
+ bx +c = 0 then,
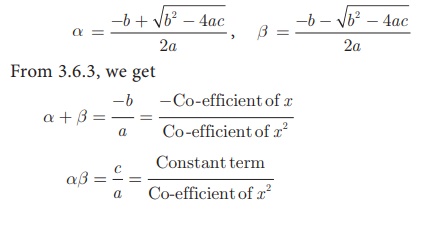
Example 3.44
If the difference between the roots of the equation x2 − 13x + k = 0 is 17 find k.
Solution
x2 − 13x + k =0 here, a = 1,
b = −13 , c = k
Let , α, β be the roots of the equation.
Then
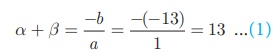
Also α – β = 17 ….(2)
(1)+(2) we get, 2α = 30 gives α = 15
Therefore, 15 + β = 13 (from (1)) gives β = −2
But, αβ = c/a = k/1 gives 15 × (−2) = k we get, k
= −30
Example 3.45
If α and β are the roots of x2 + 7 x + 10 = 0 find the values of
(i) (α - β)
(ii) α2 + β2
(iii) α3 - β3
(iv) α4 + β4
(v) α/β + β/α
(vi) α2/
β2 + β2/α2
Solution
x 2 + 7 x + 10 = 0
here, a = 1, b = 7 , c =10
If
α and β are roots of the equation then,
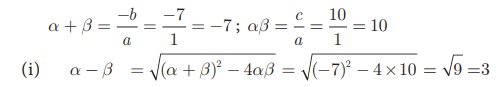
(ii) α 2 + β2
= (α + β)2 − 2αβ = (−7)2 − 2 × 10 =
29
(ii) α3 - β3 =
(α − β)3 + 3αβ(α − β) = (3)3
+ 3(10)(3) =117
(ii) α 4 + β4 =
(α 2 + β2 )2 − 2α 2
β2 = 292 - 2×(10)2 = 641 (since from
(ii)), α 2 + β2 = 29
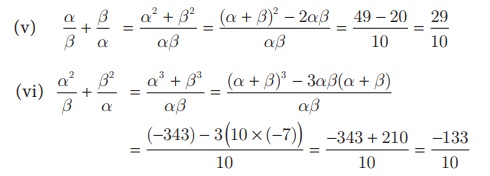
Example 3.46
If α , β are the roots of the equation 3x2 +
7 x − 2 = 0 , find the values of
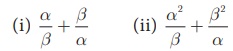
Solution
3x2 + 7 x − 2 = 0 here, a = 3 , b
= 7 , c = −2
since, α , β are the roots of the equation
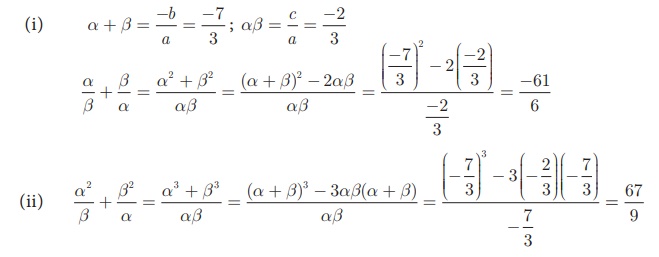
Example 3.47
If α , β are the roots of the equation 2x2 − x
−1 = 0 , then form the equation whose roots are
(i) 1/α , 1/β
(ii) α 2β , β 2α
(iii) 2α + β , 2β + α
Solution
2x2 − x −1 = 0 here, a = 2 , b = −1 , c
= −1
α + β = −b/a = −(−1) / 2 = 1/2 ; αβ = c/a =
−1/2
(i) Given roots are 1/α , 1/β
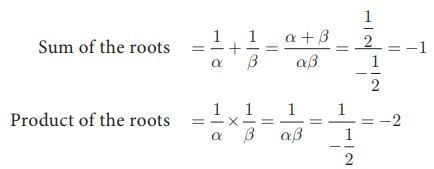
The required equation is x2 –(Sum of the roots)x
+ (Product of the roots) = 0
x 2 − (−1)x − 2 = 0 gives x2
+ x − 2 = 0
(ii) Given roots are α2 β , β2
α
Sum of the roots α2β
+ β2α = αβ(α+β) = -1/2(1/2) = -1/4
Product of the roots (α2β)
× (β2α) = α3β3 = (αβ)3
= (-1/2)3 = -1/8
The required equation is x2 - (Sum of the roots)x
+ (Product of the roots)=0
x2 –
(-1/4) x – 1/8 = 0 gives 8x2 + 2x – 1 =0
(iii) 2α + β , 2β + α
Sum of the roots 2α + β + 2β + α = 3(α + β) = 3(1/2) = 3/2
Product of the roots = (2α + β )(2β + α)
= 4αβ + 2α 2 + 2β2 + αβ
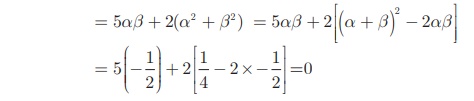
The required equation is x2 - (Sum of the roots)x
+ (Product of the roots)=0
x2 – 3/2 x + 0 = 0 gives
2x2 − 3x = 0
Related Topics