Order of a Matrix

Order of a Matrix

If a matrix A has m number of rows and n number of columns, then the order of the matrix A is (Number of rows)×(Number of columns) that is, m×n .We read m×n as m cross n or m by n. It may be noted that m×n is not a product of m and n.

General form of a matrix A with m rows and n columns (order m×n ) can be written in the form

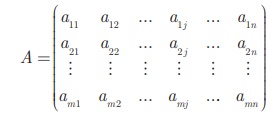
where, a₁₁ , a₁₂,... denote entries of the matrix. a₁₁ is the element in first row, first column, a₁₂ is the element in the first row, second column, and so on.

In general, a_ij is the element in the i^th row and j ^th column and is referred as (i,j)^th element. 

With this notation, we can express the matrix A as A = (a_ij )_{m ×n} where i = 1, 2,....m and j = 1, 2,...n .

The total number of entries in the matrix A = (a_ij )_{m ×n}  is mn.

Note

When giving the order of a matrix, you should always mention the number of rows first, followed by the number of columns.

For example,