Solving a Quadratic Equation by Formula Method

Solving a Quadratic Equation by Formula Method

The formula for finding roots of a quadratic equation ax² + bx +c = 0 (derivation given in section 3.6.2) is 

Example 3.33

Solve x² + 2x − 2 = 0 by formula method

Solution 

Compare x² + 2x − 2 = 0 with the standard form ax² + bx +c = 0

a = 1, b = 2, c = -2

substituting the values of a, b and c in the formula we get,

Therefore, x = −1 + √3 ,  −1 − √3

Example 3.34

Solve 2x² − 3x − 3 = 0 by formula method.

Solution

Compare 2x²  − 3x − 3 = 0 with the standard form ax² + bx + c = 0

substituting the values of a, b and c in the formula we get,

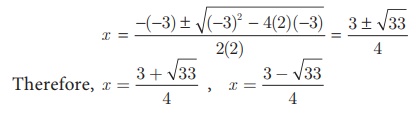
Example 3.35 Solve 3p² + 2√5p – 5 = 0  by formula method

Solution 

Solution Compare 3p² + 2√5p – 5 = 0 with the Standard form ax² + bx +c = 0

 a = 3, b = 2√5, c = −5 .

 p = (−b ± √[b² − 4ac]) /  2a

 substituting the values of a, b and c in the formula we get,

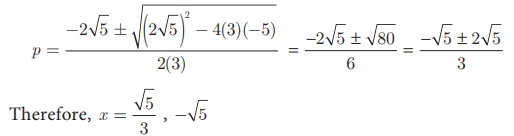
 x = √5/3 , - √5

Example 3.36

Solve pqx ² − ( p +q)² x + ( p +q)²  = 0

Solution

Compare the coefficients of the given equation with the standard form ax ² + bx +c = 0

 a = pq , b = −(p +q)² , c = ( p +q)²

substituting the values of a, b and c in the formula we get,