Exercise 3.13: Nature of Roots of a Quadratic Equation

Exercise 3.13

1. Determine the nature of the roots for the following quadratic equations

(i) 15x 2 + 11x + 2 = 0

(ii) x 2 − x −1 = 0

(iii) √2t2 − 3t + 3√2 = 0

(iv) 9y2 − 6√2y + 2 = 0

(v) 9a2b2x 2 − 24abcdx + 16c2d2  = 0 , a ≠ 0 , b ≠ 0

2. Find the value(s) of ‘k’ for which the roots of the following equations are real and equal. 

(i) (5k − 6)x2 + 2kx + 1 = 0

(ii) kx 2 + (6k + 2)x + 16 = 0

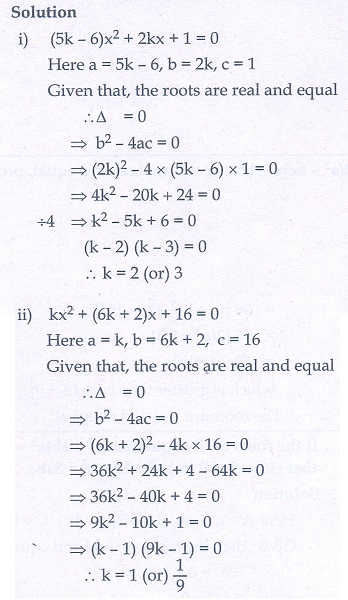
3. If the roots of (a − b )x2 + (b − c )x + (c − a ) = 0 are real and equal, then prove that b, a, c are in arithmetic progression.

4. If a, b are real then show that the roots of the equation (a − b )x2 − 6(a + b )x − 9(a −b) = 0 are real and unequal.

5. If the roots of the equation (c2 − ab)x 2 − 2(a2 − bc)x +b2 − ac = 0 are real and equal prove that either a=0 (or) a 3 + b 3 +c3 = 3abc

Answers:

1.(i) Real and unequal (ii) Real and unequal (iii) Not real (iv) Real and equal (v) Real and equal 

2.(i) 2, 3 (ii) 1, 1/9