Example Solved Problem - Addition and subtraction of matrices | 10th Mathematics : UNIT 3 : Algebra
Chapter: 10th Mathematics : UNIT 3 : Algebra
Addition and subtraction of matrices
Operations on Matrices
In this section, we shall discuss the addition and subtraction of
matrices, multiplication of a matrix by a scalar and multiplication of
matrices.
Addition and subtraction of matrices
Two matrices can be added or subtracted if they have the same
order. To add or subtract two matrices, simply add or subtract the
corresponding elements.
For example 
If A = (aij ) , B = (bij
) , i = 1, 2, ... m , j = 1,
2, ... n then C = A + B is such that C = (cij ) where cij =
a ij +bij for all i = 1, 2,
... m and j = 1, 2, ... n
Example 3.57
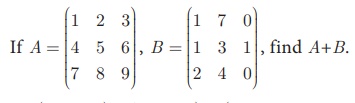
Solution
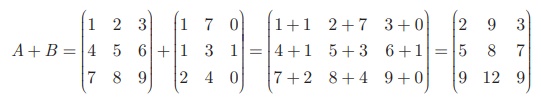
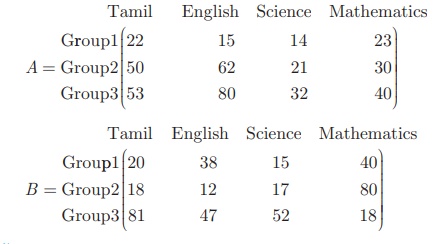
Example 3.58
Two examinations were conducted for three groups of students
namely
group 1, group 2, group
3 and their data on average of marks for the subjects Tamil, English, Science
and Mathematics are given below in the form of matrices A and B.
Find the total marks of both the examinations for all the three groups.
Solution
The total marks in both the examinations for all the three groups
is the sum of the given matrices.
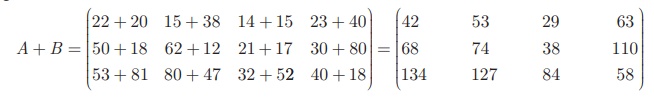
Example 3.59
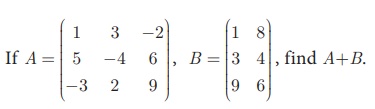
Solution
It is not possible to add A and B because they have
different orders.
Multiplication of Matrix by a Scalar
We can multiply the elements of the given matrix A by a
non-zero number k to obtain a new matrix kA whose elements are
multiplied by k. The matrix kA is called scalar multiplication of
A.
Thus if A = (aij )m ×n
then , kA = (kaij )m ×n
for all i = 1,2,…,m and for all j = 1,2,…,n.
Example 3.60
If A = 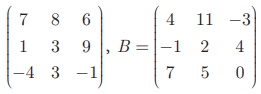 then Find 2A+B.
then Find 2A+B.
Solution
Since A and B have same order 3 ×3 , 2A + B
is defined.
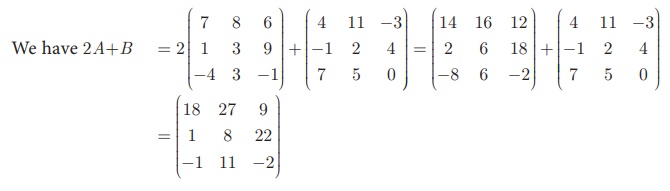
Example
3.61
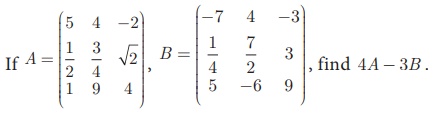
Solution
Since A, B are of the same order 3 ×3 , subtraction of 4A
and 3B is defined.
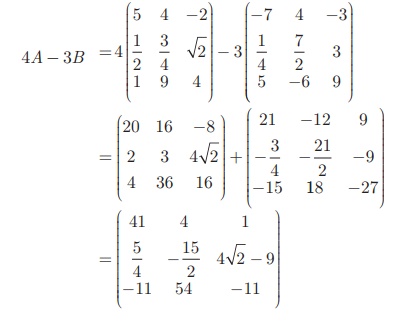
Related Topics