The Stimulus: Sound

The Stimulus: Sound

What is the stimulus for hearing? Outside in the world, some physical object is moving—perhaps an animal scurrying through the underbrush, or a set of vocal cords vibrating. This movement agitates the air particles that surround the moving object, causing these particles to jostle other particles, which in turn jostle still other particles. The actual movement of these particles is slight (about one-billionth of a centimeter) and short-lived; the particles return to their original position in a few thousandths of a second. But the motion is enough to create a momentary pressure that pushes outward from the moving object in a pattern similar to the ripples that are set in motion by a stone thrown into a pond.

If the movement continues for even a short time, it will create a series of pressure vari-ations in the air. When these sound waves hit our ears, they initiate a set of further changes that ultimately trigger the auditory receptors. The receptors in turn trigger neu-ral responses, which eventually reach the brain and lead to the experience of hearing.

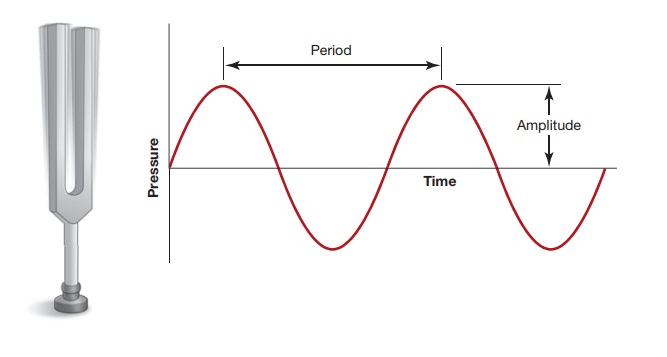
Sound waves vary in many ways; but, in the simplest case, they take the form shown in Figure 4.16. This is, for example, the pattern that would result if a tuning fork were

vibrating back and forth, pushing on the air molecules next to it each time the vibration moves the fork in one direction, and then pulling back on the same air molecules a moment later when the vibration moves the fork in the other direction. That’s why the pressure rises and falls as time goes by, in correspondence to the pushes and pulls the tuning fork is creating. (A vibrating guitar string or a vibrating clarinet reed have roughly the same effect, although these instruments produce a more complex pattern than the one shown in the figure; other movements—like the sound of a voice—would produce still more complex patterns.)

The pattern shown in Figure 4.16 is produced by a physical vibration and corre-sponds exactly to the plot of the trigonometric sine function, so this wave can be accu-rately labeled a sine wave. To describe the wave more precisely, we need to specify two things. First is the amplitude—the amount of pressure exerted by each air particle on the next. As the figure shows, this pressure is constantly changing as the air molecules vibrate toward each other, then away, then toward again. Thus, the amplitude we actu-ally measure is the maximum pressure achieved at the crest of the sound wave. Second, we need to specify how widely spaced these pressure crests are. We could do this in terms of wavelength—a measurement of the distance between one crest and the next— or in terms of period, a measure of how much time elapses between one crest and the next. When measuring sounds, it’s usually more convenient to take the inverse of the period; so, instead of measuring seconds per crest, we measure crests per second, which is the frequency of the wave. This means our measure is literally a count of how many times in each second the wave reaches its maximum amplitude (Figure 4.17).

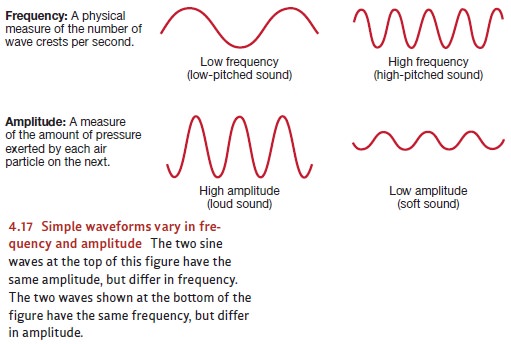
Amplitude and frequency are physical dimensions of the sound wave itself, but they cor-respond reasonably well to the psychological dimensions of loudness and pitch. Roughly speaking, a sound will be heard as louder as its amplitude increases. It turns out that humans can respond to an enormous range of amplitudes, so investigators find it useful to measure these intensities with a logarithmic scale, which compresses the range into a more convenient form. Specifically, sound intensities are measured in decibels, and they’re always assessed in relation to some standard. A standard of zero decibels is often assumed to be the average detection threshold for an adult with normal hearing. Loudness doubles each time the intensity of a sound increases by 10 decibels (Stevens, 1955).

The frequency of a sound wave is measured in cycles per second, or hertz (named after the 19th-century physicist Heinrich Hertz). As frequency increases, the subjective pitch of the sound goes up. Middle C on a piano generally has a frequency of 261 hertz; the C an octave higher has a frequency of 522 hertz. (In general, a doubling of frequency produces the experienced pitch difference of one octave.) The frequencies associated with other musical tones are shown in Table 4.3. Young adults can hear tones as low as 20 hertz and as high as 20,000 hertz. As people get older, their sensitivity to sound declines— especially at the higher frequencies. For this reason, sometimes there’s little point for a

30- or 40-year-old to buy expensive stereo equipment, since what makes the equipment expensive is often its exquisite ability to reproduce high frequencies accurately! In many cases, the middle-aged stereo buyer will be deaf to these frequencies and so probably won’t be able to tell the difference between the expensive stereo and a cheaper one.

So far, we’ve been talking only about sine waves; but we rarely encounter sine waves in our everyday lives. Instead, the sound waves we usually experience are far more complex. Figure 4.18A, for example, shows the moment-by-moment changes in air pressure produced by a few seconds of music; Figure 4.18B shows the moment-by-moment pressure changes produced by a bit of ordinary speech.

The mathematician Joseph Fourier was able to show that these complex waves are actually just the sum of simpler components—in particular, the sum of a series of sine waves. Essentially, we can think of sine waves as the “ingredients” that combine to pro-duce more complicated sounds. The “recipe” for creating the more complex sound must

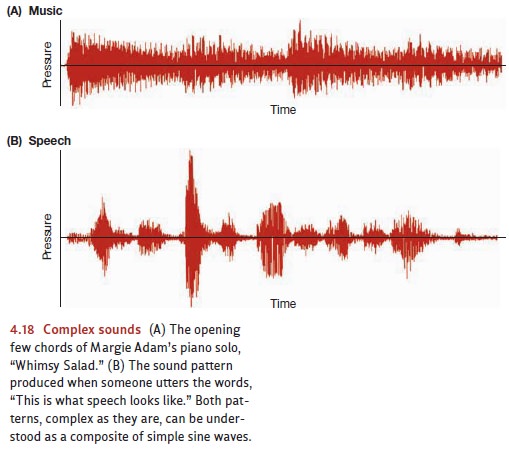
identify which ingredients are to be used (i.e., which frequencies) and how much of each ingredient is needed (i.e., how much amplitude for each of the frequencies is mixed into the whole). But once that’s done, we can use the recipe to create any sound we choose from sine-wave ingredients. Psychologists as well as physicists, audio engi-neers, and many others routinely use Fourier analysis to describe in detail the sounds we encounter in our day-to-day experience.