The Neural Basis of Color Vision

The Neural Basis of Color Vision

What is the neural basis of color vision? The answer turns out to have two parts: how the retina itself functions, and how the nervous system handles the information received from the retina.

COLORRECEPTORS

More than 200 years ago, Thomas Young hypothesized that humans have three types of color receptors; and he offered a theory of color vision building on these three ele-ments. In 1866, Hermann von Helmholtz offered some refinements of this view. Today we know that, at least in broad outline, the Young-Helmholtz theory was essentially correct. Human color vision is trichromatic—based on three elements, each tied to one type of cone.

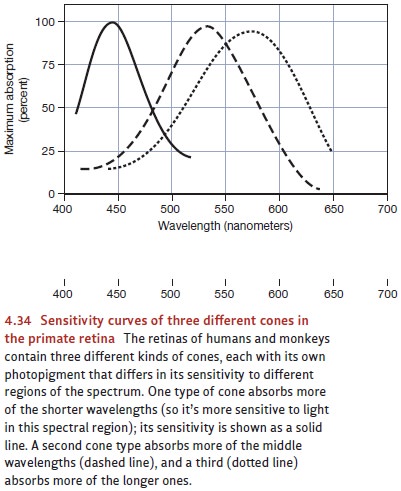
What are these “elements”? We’ve already mentioned that each of the three cone types contains a different photopigment. Each of these photopigments is sensitive to a broad range of wavelengths, but their patterns of sensitivity are plainly distinct (Figure 4.34). One pigment, and so the cones containing that pigment, is most sensitive to wavelengths in the short-wave region of the spectrum. Consequently, this pigment is sensitive to many inputs but especially sensitive to wavelengths typically perceived as blue. A second pigment is especially sensitive to wavelengths in the middle range (wavelengths typically perceived as green), and the third to wavelengths in the long range (typically perceived as orange or red; Bowmaker & Dartnall, 1980; MacNichol, 1986).

It’s important to realize that due to the broad sensitivities of these pigments, all three types of cones respond to most of the wavelengths in the visible spectrum. It’s therefore impossible to discriminate among wavelengths simply by noting which

cones are responding, because generally all of them are. So once again, it appears that the nervous system relies on pattern coding; the input’s wavelength is being specified by the relative rates of response by all three cone types. For an input of 480 nanome-ters, for example, the “short-preferring” and “middle-preferring” cones will respond equally, and their response will be about double the response of the “long-preferring” cones. This pattern of response specifies this particular wavelength. Likewise, an input of 580 nanometers will produce a response in the long-preferring cones that’s roughly double the response in the middle-preferring cones, and there will be virtually no response from the short-preferring cones. This pattern identifies this specific wave-length. And so on for the millions of other response patterns, each of which identifies a specific wavelength.

Of course, many of the colors you encounter involve a mix of several different wavelengths; but that’s not a problem. Each of the wavelengths contained in this mix will trigger the neural response that would result if that wavelength were presented on its own, and so the total response for each cone type will simply be the sum of that cone’s responses to each ingredient—each wavelength—in the mix. Here’s an example: If the input contains wavelengths A, B, and C, the short-preferring cones’ response to this stimulus will simply be the total of those cones’ response to A when it’s presented alone, plus their response to B when it’s presented alone, plus their response to C. (And so if, say, the light is at an intensity in which wavelength A on its own would trigger the receptor to fire 70 times per second, and B on its own would trigger the receptor to fire 30 times per second, and C would trigger the cell to fire 10 times per second, the mix of A, B, and C will cause the cell to fire roughly times per second.) The same goes for the middle-preferring and long-preferring cones; their responses, too, will simply be the sums of their responses to each of the individual ingredients in the mix.

Be aware, though, that it’s the total response that matters—not how the total was achieved. Thus, if three wavelengths together cause the short-preferring cones to fire times per second, it doesn’t matter if the wavelengths on their own would have produced rates of 70, 30, and 10 (as in the previous paragraph), or if they would have produced rates of 20, 60, and 30 or 37, 15, and 58. All that matters is the sum. And this is crucial, because it’s almost always possible to find different mixes of wavelengths that will produce the same three totals (again, one total for each of the cone types). This explains why artists can mix their pigments to produce virtually any color, and it’s how a television or computer monitor produces the various colors that appear on the screen. In both of these cases, we’re combining wavelengths so that we’ll get the three totals we need to produce the desired perception.

COMPLEMENTARY HUES

The trichromatic analysis of color vision is consistent with many facts—including the central observation that there are just three cone types, each with its own photopig-ment. Other observations, however, don’t seem to fit with the trichromatic view—such as the fact that, in important ways, colors seem to come in pairs. This pairing is evident, for example, in simultaneous color contrast—the chromatic counterpart of brightness contrast. Color contrast refers to the tendency of any chromatic region in the visual field to induce a complementary color in adjoining areas. For example, a gray patch tends to look bluish if it’s surrounded by yellow, and yellowish if surrounded by blue; likewise, a gray patch looks reddish if surrounded by green, and greenish if surrounded by red (Figure 4.35). In this way, then, blue and yellow are “paired,” as are red and green.

Color contrast can also be demonstrated in temporal relationships rather than spatial ones. Suppose that you stare at a green patch for a while and then look at a white wall. You’ll see a negative afterimage of the patch—in this case, a reddish spot (Figure 4.36). In the same way, staring at a red patch will produce a green afterimage; staring at some-thing blue will produce a yellow afterimage; and staring at yellow will produce a blue afterimage. In all cases, the afterimage has the comple-mentary hue of the original stimulus. This effect again emphasizes the apparent pairing of colors—a pairing that trichromatic analyses leave completely unexplained.

Another way to appreciate the importance of complementary col- ors is by mixing together colored lights. In these mixtures, “paired” colors seem to can-cel each other; thus, if we mix blue and yellow lights, we produce a hueless white. The same is true if we mix red and green lights, or purple and yellow-green, or orange and blue-green. Here, too, it appears that colors are paired, such that each color has an “opposite” that cancels it—a relationship that, again, has no explanation in trichro-matic theory.

As an aside, note that color mixing works differently when we mix paints or other pig-ments rather than lights (as in Figure 4.37). Why? Because of the physics. Here’s an example: If a blue light is shining on a white surface, then the surface will reflect the wavelengths contained within that blue light. If a yellow light is also shining on the surface, then its wavelengths will be reflected too. So the full set of wavelengths reflected will be those from the blue light plus those from the yellow—which is why this is called an additive color mixture. In contrast, when white light shines on a pigment, only a certain band of wavelengths is reflected; the remaining wavelengths are absorbed by the pigment. Thus blue paint reflects the wavelengths between 420 and 520 nanome-ters, but it absorbs wavelengths outside this range; and so these other wavelengths are removed or “subtracted” from the reflected light. Yellow paint reflects wavelengths above 480 nanometers, and it absorbs those below. If the two paints are mixed together, then the only wavelengths reflected by the combination are those that aren’t absorbed (i.e., not subtracted from the input) by either ingredient. This mixture turns out to be just the wavelengths above 480 nanometers and below 520; and that band of wavelengths is seen as green.

THE  OPPONENT- PROCESS  THEORY

How should we think about the fact that colors seem to come in pairs? The answer ies  in  the  opponent-process  theory,  first  suggested  by  Ewald  Hering  but  then developed by Leo Hurvich and Dorothea Jameson. This theory begins with the unde- niable  fact  that  we  have  three  cone  types, but  it  argues  that  the  output  from  these cones is then processed by another layer of neural mechanisms that recode the sig- nal on the basis of  three pairs of  colors—red versus green, blue versus yellow, and black versus white. 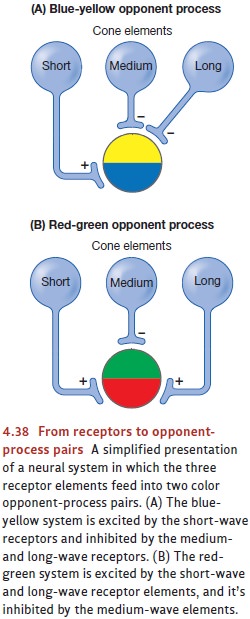These pairs are said to involve an “opponent process” because the two members of each pair are antagonists—that is, excitation of neurons on one side of these mechanisms automatically inhibits cells on the other side (Figure 4.38). As a result, each of the opponent-process mechanisms can be thought of as a balance— and if one arm of the balance goes down, the other necessarily goes up (Hurvich &Jameson, 1957).

How do these mechanisms shape our perception of color? According to the opponent- process theory, the psychological experience of  hue depends on two of  the opponent- process pairs—red-green and blue-yellow. If, for example, the input tips the red-green balance toward red and the blue-yellow balance toward blue, the perceived hue will be violet. If the input contains neither red nor green (so the red-green pair stays in balance) and the blue-yellow system tips toward blue, we perceive a pure blue. If both hue systems are in balance, there will be no hue at all, and the resulting color will be seen as achro- matic (i.e., without hue).

This conception easily explains the apparent pairing of colors, because the pairing is built into the opponent processes themselves. It also explains why, according to most observers, there appear to be four primary colors (red, green, blue, and yellow)—even though,  without  question,  our  retina  has  only  three  cone  types.  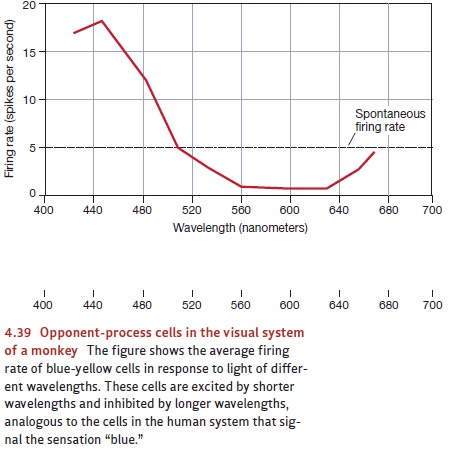But,  in  addition, evidence  has  directly  confirmed  the  claims  of  the  opponent-process  theory  by  docu- menting that many of the neurons in the visual system behave exactly as the theory pro- poses. For example, certain cells increase their firing rate if the retina is stimulated by green light, but they decrease their rate if the retina is stimulated by red light. Other cells show the opposite pattern (increase for red, decrease for green). Still other cells show a similar pattern of responses for blue and yellow light (Figure 4.39; De Valois, 1965). All of this is exactly what we might expect if these cells embody the mechanisms proposed by the opponent-process theory.

COLOR BLINDNESS

Not everyone responds to color like most of us do. Some form of color-vision defect is found in 8% of Caucasian males (but only 0.03% of females; the rate of color blindness is lower in other races). The deficiencies in color vision come in various forms. The great majority of people identified as color blind are actually missing one of the three visual pigments (and so they’re “dichromats,” not “trichromats”). Other forms of color blind-ness can involve a defective opponent process or a malfunction in brain circuitry needed for color vision (Hurvich, 1981). Most common is a confusion of reds with greens; least common is total color blindness, in which no hues can be distinguished at all. Interestingly, though, most of these problems are rarely noticed in everyday life, and color-blind people can spend many years without even realizing they’re color blind. They call stop signs “red” and grass “green,” just like anyone else does. 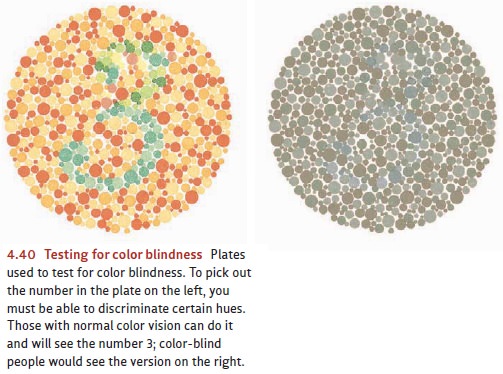And, presum-ably, they spend much of their lives believing that others perceive colors the same way they do. Their color blindness can be confirmed only with special tests like the one shown in Figure 4.40.

Color blindness can result from various injuries to the eye or brain, but this condi-tion most commonly has a genetic origin. It’s also much more frequent in humans than it is in other primates with color vision similar to our own. This finding has led some scholars to explore the evolutionary origins of color blindness. They argue that this supposed “defect” might actually have benefited some of our evolutionary ancestors— for example, in certain situations a color-blind hunter can spot prey that others might miss. (Because hues that appear “matched” to someone with normal color vision sometimes don’t appear matched for someone who is color blind, some forms of cam-ouflage—when the prey seems to be the same hue as the background foliage—will fail with someone who is color blind.) These situations might have produced a reproduc-tive advantage for our color-blind ancestors, leading to an increased frequency in the relevant human genes.

Recent studies indicate that the genetics of color blindness are relatively complex and that many genes, on at least 19 different chromosomes, can contribute to color blindness. One of the genetic causes involves a gene mutation on the X chromosome, and this finding explains why color blindness is much more common in men than in women. Women have a pair of X chromosomes, so at least one of the chromosomes in this pair is likely to have a normal version of the relevant gene—leading to normal color vision. Men have an XY genetic pattern, and so only one X chromosome. If this chromosome contains the mutated gene, men have no “backup” gene on another chromosome—and color blindness is the result.

How does the world look to someone who is color blind? For a long time, this ques-tion seemed impossible to answer, since most color-blind individuals have no way to compare their experience to that of an individual with normal color vision, and so no way to describe the difference. However, researchers discovered one unusual person (one of the rare women with a color-vision defect) who was red-green color-blind in one eye but had normal color vision in the other. She was able to describe what she saw with the defective eye by using the color language she had learned to use with her other eye. As she described it, with the color-blind eye she saw only grays, blues, and yellows. Red and green hues were altogether absent, as if one of the opponent-process pairs were missing (Graham & Hsia, 1954).