Psychophysics: Sensory Thresholds

Sensory Thresholds

We can apply the methods of psychophysics to several different questions as well as a wide range of stimuli. Picture this: You’re in a restaurant, eating a particularly tasty fish. Knowing you’d like to re-create the dish in your own kitchen, you might ask, “What’s the source of that distinctive flavor?” Here you’re asking a psychophysical question— what was it in the physical stimulus that led to a particular sensation, a particular taste? You might realize that the flavor came from adding a tiny bit of saffron to the fish, and so you decide to use saffron in your own cooking. But saffron is the world’s most expen-sive spice, so you’d like to add as little as possible. How much saffron do you need—so that people tasting the fish will just pick up the hint of saffron? This is a psychophysi-cal question about people’s ability to detect an input. And perhaps you try the dish once, and decide that next time the saffron flavor could be a tiny bit stronger. How much saf-fron should you add to produce that stronger flavor? This, too, is a psychophysical question—about the ability to detect differences.

Let’s start our examination of psychophysics, therefore, with the issue of detection: To continue the example, when we try to determine the smallest amount of saffron you can use (so that you get the effect of the spice without straining your budget), we’re asking a question about an absolute threshold—the smallest quantity of an input that can be detected. The absolute threshold is assessed in precise physical terms—the number of strands of saffron needed; or the amount of light, measured in quanta, needed for someone to see the light; or the loudness, measured in sound pressure levels, needed for someone to hear a sound. However, we can translate these thresholds into common-sense terms—and when we do, it’s clear that our thresholds for many stimuli are very low indeed (Table 4.1).

Our cooking example also highlighted a different type of detection—namely, the detection of differences. If we add two more strands of saffron, can we detect this alter-ation in the stimulus? How about five more grains, or ten? These are questions about someone’s difference threshold—the smallest change in an input that can be detected. When a stimulus is changed by this minimal amount, psychophysicists call it a just-noticeable difference, or jnd. We can measure thresholds for many different sensory dimensions—flavors, brightness, loudness, smells, heaviness, pressure, and more. Across all of these dimen-sions, difference thresholds show a consistent property: They depend on proportional

differences, and not absolute differences. To illustrate, let’s say that you can tell the dif-ference between a backpack filled with 25 pounds of camping gear and one that con-tains a half-pound more—and so 25.5 pounds. This does not mean that, in general, you’re sensitive to half-pound differences. What matters instead is the proportional change—in this case, a difference of 2%. Thus, you probably would not be able to distinguish between a backpack filled with 50 pounds of gear and one that contains 50.5 pounds. This is still a half-pound difference, but only a 1% change. But you would be able to distinguish 50 pounds from 51, or 75 pounds from 76.5—in each case a 2% difference.

This important role for proportions, first documented by the 19th-century physiolo-gist E. H. Weber, is known as Weber’s law. Put algebraically, this law is written as

In the equation, I is the intensity of the standard stimulus, the one to which comparisons are being made; I is the amount that must be added to this intensity to produce a just-noticeable increase; c is a constant (in our example, it was .02, or 2%). The fraction I  /I  is referred to as the Weber  fraction.

Weber’s law is important for several reasons, including the fact that it allows us to compare the sensitivities of different sensory modalities. Suppose we want to know whether the eye is more sensitive than the ear. We cannot compare jnds for brightness and loudness directly; the first is measured in millilamberts, the second in decibels, and there’s no way to translate the one into the other. But we can compare the Weber frac-tions for the two modalities. If the fraction for a specific sense modality is small, then we know that the modality is able to make fine discriminations; that is, it will detect even small percentage changes. 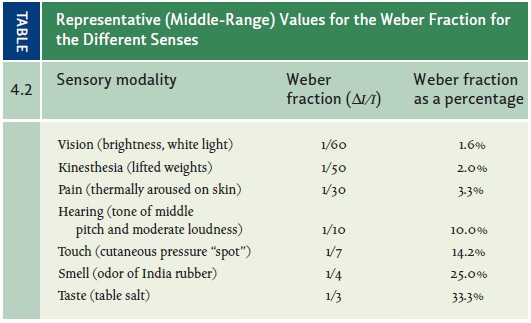And, of course, the smaller the Weber fraction, the more sensitive the sense modality. Using these comparisons, we can show that we are much keener at discriminating brightness (we’re sensitive to differences of merely 1.6%) than weight (2%), and more sensitive to differences in weight than we are to differences in loudness (10%). The Weber fractions needed for this comparison, and fractions for other sense modalities, are presented in Table 4.2.

Weber’s law also helps us solve a further puzzle: The measurement of difference thresholds tells us whether the perceiver can detect a change or not. Often, though, we want to know more than this. We want to know about the perceiver’s experience—how bright does the light seem to the perceiver, or how loud does the sound seem? Then we

want to link these measurements to the stimulus, so that we can specify the correspon-dence between the intensity of the stimulus and the intensity of the experience.

More than a hundred years ago, Gustav Fechner was able to address this issue mathe-matically, building on Weber’s law. His result, often referred to as Fechner’s law, describes the relationship between the physical intensity of a stimulus and the psychological inten-sity of the experience produced by that experience. The law states that the strength of a sensation increases logorithmically with the intensity of the stimulus. Formally, the law is written:

S = k log I

In the equation, S stands for psychological (i.e., subjective) magnitude; I is the physical intensity of the stimulus; and k is a constant whose value depends on the value of the Weber fraction.

In the years since Fechner we’ve learned that, in truth, this law does not hold up perfectly in all circumstances. (For example, the perception of pain does not show the pattern predicted by Fechner ’s law; for pain, a very small increase in the stimu-lus causes a large increase in the sensation—a pattern that’s useful in compelling us to deal with pain when it arises.) For our purposes, though, the law does hold in a wide range of settings and with a diversity of stimuli. It offers a reasonably accu-rate characterization of the relationship between stimulus intensity and subjective impression.