Psychophysics: Detection and Decision

Detection and Decision

Sensory thresholds are defined in terms of stimulus intensities—how much intensity do we need before we can detect the stimulus? How much of a change in intensity do we need to detect that two stimuli are different? It turns out, however, that these inten-sities are not the only factors determining how someone responds in a psychophysical experiment. Indeed, even this early in our description of the sensory processes, we need to realize that we’re not trying to understand how light meters or audiometers work. Instead, we’re discussing the capacities and behaviors of living organisms—and that introduces some complications.

To illustrate, imagine a pair of research participants, Matt and Fiona. Matt says, “Yes, I heard that one,” in response to most of the barely audible tones being pre-sented by the experimenter. Fiona, in contrast, says yes to only a few of the tones, and she insists that she couldn’t hear anything at all on the remaining test trials. One interpretation of this pattern is that Matt has more acute hearing than Fiona does; they differ, in other words, in their perceptual sensitivity. A different possibility, though, is that Matt and Fiona differ only in their decision criteria—that is, in the “cutoff ” they use for deciding when to say yes and when to say no. Maybe Matt is a bit of a risk taker. Or perhaps he has always thought of himself as having acute hearing, and this leads him to put more trust in the vague feeling that he might have just heard the tone. For either of these reasons, Matt may—without even realizing it—adopt an attitude of “When in doubt, say ‘Yes, I heard that one.’” Fiona, on the other hand, might be more cautious; or she might be worried that the experimenter will think she’s careless if she says yes too often. To avoid this danger, she slips into a more conserva-tive attitude: “When in doubt, say ‘No, I didn’t hear that one.’” If any of these inter-pretations are correct, then the difference between Matt’s and Fiona’s responding might not reflect a difference in their hearing; instead, it shows only that they handle uncertainty in different ways.

SIGNAL – DETECTION PROCEDURES

Variations in decision criteria add a layer of extra complexity to our discussion of sensory thresholds, but signal-detection theory allows us to deal with this complexity. In a signal-detection procedure, the experimenters present a faint target stimulus on some trials but no stimulus on other trials. This procedure allows the experimenters to ask how often the participant gives each of the four possible types of response. One response type is a hit—the participant says, “Yes, I detected the target” when there really was one. A second type is a false alarm—the participant says, “Yes, I detected the target” when there was none. A third response type is a correct negative—saying “No target” when this is in fact the correct answer. The final type is a miss—saying “No target” even though one was actually presented (Figure 4.5).

To see how this information can be used, let’s continue with the example of Matt and Fiona. We’ve already said that Matt has a higher hit rate than Fiona does, and we’ve noted that this observation is, by itself, ambiguous: Perhaps Matt’s hearing is more sen-sitive than Fiona’s, or maybe he’s just more casual in his responding and relies on a rel-atively loose criterion. Based on hit rates alone, there’s no way to tell these possibilities apart. A signal-detection experiment, though, provides other information, and this allows us to figure out what’s going on with these two participants. Let’s say that, in fact, Matt does have a low criterion for responding, and that’s why he usually says yes to each of the faint signals. The same low criterion, though, will encourage Matt to say yes even when no signal is presented; those trials, too, will often satisfy his rule of “When in doubt, say ‘Yes, I heard that one.’” So Matt will, as we’ve said, have a high hit rate; but he’ll also have a relatively high false-alarm rate. His responses, in other words, will tend to be in the two cells in the left-hand column of Figure 4.5.

In contrast, let’s suppose that Matt’s hit rate is high because he really does have excel-lent hearing and can detect each of the subtle signals. In that case, Matt probably won’t be fooled by the stimulus-absent trials; his acute hearing will allow him to realize that these trials contain no stimulus, and so he’ll correctly respond “no” to these trials. Therefore, his false-alarm rate will be low, and his responses overall will accumulate in the top left and bottom right cells of Figure 4.5.

These points set the pattern for a signal-detection analysis. In general, if individuals differ in how sensitive they are to the signal, then they’ll differ in their proportions of correct and incorrect responses—their total number of hits and correct negatives rela-tive to their total number of misses and false alarms. But if individuals differ in their response criterion (e.g., whether they say yes when in doubt, or no), then they’ll differ in their proportions of yes and no responses. (Of course, it’s possible for participants to differ in both their sensitivity and their criterion; but, with a bit of algebra, we can dis-entangle these effects from the signal-detection data.) By looking at all of the numbers, therefore (i.e., by looking at hits, misses, false alarms, and correct negatives), we can cal-culate two measures for each person. We can, first, measure the person’s sensitivity to the input—and, for most purposes, this is the measure we want. Second, we can measure the person’s criterion—and so gain a measure of how much information the person needs before saying, “Yes, I heard it” (or saw it or smelled it or whatever).

People differ in their sensitivity for various reasons: For example, a 20-year-old’s hearing is typically more sensitive than a 50-year-old’s because of the age-related decline in hearing. A 20-year-old who listens to a lot of loud music will have less sen-sitive hearing than someone who listens to quieter music, because the ear is damaged by overstimulation. And so on.

Why do people have different response criteria? The answer involves several different factors—some of them enduring traits of the person, some of them tied to the specific circumstances. We considered some examples in our discussion of Matt and Fiona— for example, the possibility that Matt might just be a risk taker, or that he’s guided by his self-confident belief that he has good hearing. Just as important is a person’s belief about the frequency of signals. (If, for example, you believe that signals will be presented on 98% of the trials, it makes sense to adopt a rule of “When in doubt, say ‘I heard it’”—because this rule will lead to a correct response most of the time. If you believe, in contrast, that signals will be presented on only 1% of the trials, it makes sense to adopt the opposite rule.) Also crucial is the payoff matrix—the pattern of benefits and costs associated with each type of error. Imagine Matt was trying to impress the experimenter with his fine sense of hearing. In that case, Matt would put special weight on the benefits associated with a hit and the costs associated with a miss. This approach would encourage a lower criterion. Suppose Fiona, on the other hand, is worried about appearing careless; she might emphasize the costs associated with a false alarm, thus leading her to use a higher criterion.

IMPLICATIONS OF SIGNAL  DETECTION

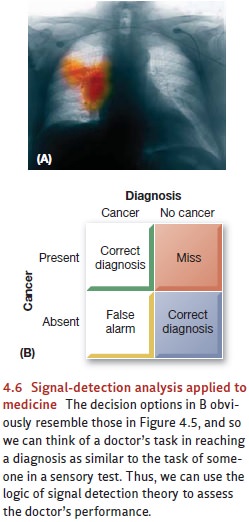
Signal-detection analysis is a valuable research method with applications in a wide range of settings. Researchers have used signal detection to study cases as diverse as the memory effects of hypnosis and the decisions made by college admissions officers. As just one example, consider the case presented in Figure 4.6. Here a doctor who is seek-ing to diagnose cancer is trying to decide whether a “signal” (the illness) is present in that patient or not, and, with the problem laid out in this way, the resemblance between the doctor’s task and, say, Matt’s or Fiona’s—as in Figure 4.5—should be obvious. Suppose we want to evaluate this doctor’s performance—maybe we’re trying to decide how much we can trust this particular doctor, or whether the doctor needs more train-ing. In all cases, we’d need to measure the doctor’s sensitivity to this “signal,” and we’d need to separate that sensitivity from the doctor’s criterion. To see how important this is, imagine a doctor who diagnoses cancer in patient after patient. This might mean the doctor is especially astute and can detect this serious problem whenever he encounters it; this sounds like a doctor one should seek out. But it might also mean the doctor has a lax criterion and offers this horrible diagnosis based on relatively thin evidence; now this sounds like a doctor to be avoided! It would obviously be useful to know which of these descriptions is correct, and of course this is precisely the information provided by signal-detection analysis. (For details on how signal detection has been applied to other domains, including medical diagnosis, see, for example, McFall & Treat, 1999; Swets, Dawes, & Monahan, 2000.)

Signal-detection analyses highlight another crucial point: We often make decisions with imperfect information, so it’s inevitable that we’ll make some errors. What can we do about this? If we are especially concerned about false alarms (a cancer test that says someone has the disease even though she doesn’t, or a jury that votes “guilty” even though the defendant is innocent), we can take steps to raise the response criterion. This adjustment will decrease the number of false alarms, but it’s likely to increase the number of misses (failing to detect an actual tumor, or acquitting someone who is actu-ally guilty). On the other hand, we could shift in the opposite direction—to a lower criterion—but this would lead to the opposite pattern of benefit and risk: Lowering the criterion will decrease the number of misses but increase the number of false alarms.

How should we think about these issues? That depends on the specific case—and, in particular, the potential consequences of a miss or false alarm. Overall, though, when we make decisions (or develop a cancer test, or instruct a jury), it’s important to remem-ber that this trade-off between misses and false alarms is in place. If we want to evalu-ate anything from a cancer test or a jury instruction to the memory effects of hypnosis or the police department’s decision about whether to take a bomb threat seriously, signal-detection analyses can provide separate measurements of sensitivity and criterion—information that allows us to ensure that these decision processes are well tuned to our goals.