Applications of Differential Calculus | Mathematics - Summary | 12th Maths : UNIT 7 : Applications of Differential Calculus
Chapter: 12th Maths : UNIT 7 : Applications of Differential Calculus
Summary
SUMMARY
ŌĆó If y =
f (x) , then dy/ dx represents
instantaneous rate of change of y with
respect to x .
If y =
f ( g (t )) , then dy/dt = f ŌĆ▓ ( g (t ))Ōŗģ gŌĆ▓ (t ) which is called the chain
rule.
ŌĆó The
equation of tangent at ( a , b) to the curve
y = f (x) is given by y ŌłÆ
b = (dy/dx)(a,b)(x ŌłÆ a)
or y-b = f ŌĆ▓ (a)(x ŌłÆ a) .
ŌĆó RolleŌĆÖs
Theorem
Let f ( x) be continuous in a closed
interval [ a , b] and differentiable on the open interval ( a , b) . If f (a)
= f (b) , then there is at least one point c Ōłł( a,b) where f ŌĆ▓ (c) = 0 .
ŌĆó LagrangeŌĆÖs
Mean Value Theorem
Let f ( x) be continuous in a closed interval
[ a , b] and differentiable on the
open interval ( a , b) (where f (a) and f (b) are not necessarily equal). Then there is at least one point
c Ōłł( a,b) such that f ŌĆ▓ (c) = f (b) ŌłÆ f (a) / b-a. 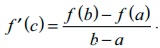
ŌĆó TaylorŌĆÖs
series
Let f ( x)
be a function infinitely differentiable at
x = a . Then f ( x) can be
expanded as a series in an interval ( x ŌłÆ a , x + a) ,of the form

ŌĆó MaclaurinŌĆÖs
series
In the
TaylorŌĆÖs series if a = 0 , then the expansion takes the form

ŌĆó The
lŌĆÖH├┤pitalŌĆÖs rule
Suppose f ( x)
and g ( x) are differentiable functions and g ŌĆ▓ ( x) ŌēĀ 0 with
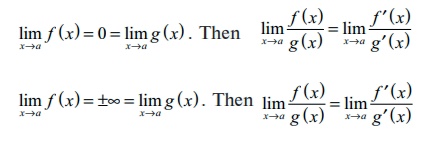
ŌĆó If the
function f ( x) is differentiable in
an open interval ( a , b) then we
say, if d/dx ( f (x)) > 0 , ŌłĆ x Ōłł( a,b) then f ( x) is strictly increasing in the interval (a,b).
ŌĆó if d/dx ( f
(x)) <
0 , ŌłĆ x
Ōłł(
a,b)
then f ( x) is strictly decreasing in the
interval ( a , b)
ŌĆó A
procedure for finding the absolute extrema of a continous function f ( x)
on a closed interval [a , b].
Step 1 :
Find the critical numbers of f (
x) in ( a , b)
.
Step 2 :
Evaluate f (
x) at all critical numbers and at the
endpoints a and b .
Step 3 :
The largest and the smallest of the values in Step 2 is the absolute maximum
and absolute minimum of f (
x) respectively on the closed interval
[a , b]
.
ŌĆó First
Derivative Test
Let (
c , f (c)) be a critical point
of function f (
x) that is continuous on an open
interval I containing c . If f ( x)
is differentiable on the interval, except possibly at c , then f (c) can be classified as
follows:(when moving across I from
left to right)
(i) If f ŌĆ▓ ( x)
changes from negative to positive at c
, then f (
x) has a local minimum f(c).
(ii) If f ŌĆ▓ ( x)
changes from positive to negative at c
, then f (
x) has a local maximum f (c).
(iii) If
f ŌĆ▓ ( x)
is positive on both sides of c , or
negative on both sides of c then f ( x)
has neither a local minimum nor a local minimum.
ŌĆó Second
Derivative Test
ŌĆó Suppose
that c is a critical point at which f ŌĆ▓ (c)
=
0 , that f ŌĆ▓ŌĆ▓
(
x) exists in a neighbourhood of c , and that f ŌĆ▓ (c) exists.
Then f has a relative maximum value
at c if f ŌĆ▓ŌĆ▓ (c) < 0 and a relative minimum value at c
if f ŌĆ▓ŌĆ▓ (c) >
0 . If f ŌĆ▓ŌĆ▓
(c) =
0 , the test is not informative.
Related Topics