Related rates

Related rates

A related rates problem is a problem which involves at least two changing quantities and asks you to figure out the rate at which one is changing given sufficient information on all of the others. For instance, when two vehicles drive in different directions we should be able to deduce the speed at which they are separating if we know their individual speeds and directions.

Example 7.7

If we blow air into a balloon of spherical shape at a rate of 1000 cm³ per second, at what rate the radius of the baloon changes when the radius is 7cm? Also compute the rate at which the surface area changes.

Solution

Therefore, the rate of change of radius is 250/49Ï€  cm/sec and the rate of change of surface area is 2000/7 cm² / sec.

Example 7.8

The price of a product is related to the number of units available (supply) by the equation Px + 3P −16x = 234 , where P is the price of the product per unit in Rupees(₹) and x is the number of units. Find the rate at which the price is changing with respect to time when 90 units are available and the supply is increasing at a rate of 15 units/week.

Solution

We have,

We have, 234+16x / x+3

Substituting x = 90, dx/dt = 15, we get dP/dt = − 186/93² × 15= − 10/31 ≈ −0 .32 rupee/week. That is the price is changing, in fact decreasing at the rate of  ₹ 0.32 per week.

Example 7.9

Salt is poured from a conveyer belt at a rate of 30 cubic metre per minute forming a conical pile with a circular base whose height and diameter of base are always equal. How fast is the height of the pile increasing when the pile is 10 metre high?

Solution

Let h and r be the height and the base radius. Therefore h = 2r . Let V be the volume of the salt cone.

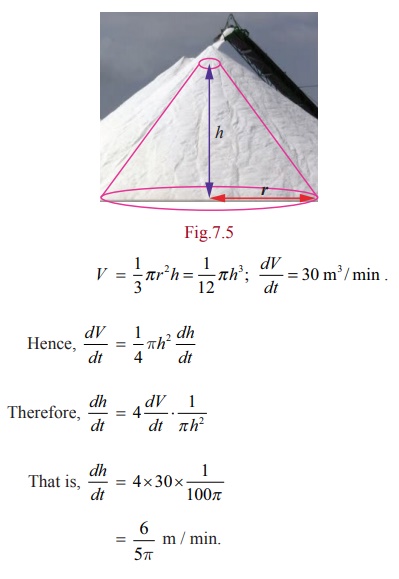
= 5/5Ï€ m / min.

Example 7.10 (Two variable related rate problem)

A road running north to south crosses a road going east to west at the point P . Car A is driving north along the first road, and car B is driving east along the second road. At a particular time car A is 10 kilometres to the north of P and traveling at 80 km/hr, while car B is 15 kilometres to the east of P and traveling at 100 km/hr. How fast is the distance between the two cars changing?

Solution

Let a (t) be the distance of car A north of P at time t , and b (t) the distance of car B east of P at time t, and let c(t) be the distance from car A to car B at time t . By the Pythagorean Theorem, c (t)² = a (t)² + b (t)² .

Taking derivatives, we get 2c (t)c’(t) = 2a (t)a’(t) + 2b (t)b’(t) .

at the time of intersect.