Differential Calculus | Mathematics - Series Expansions: MaclaurinŌĆÖs and TaylorŌĆÖs Series | 12th Maths : UNIT 7 : Applications of Differential Calculus
Chapter: 12th Maths : UNIT 7 : Applications of Differential Calculus
Series Expansions: MaclaurinŌĆÖs and TaylorŌĆÖs Series
Series Expansions
TaylorŌĆÖs
series and Maclaurin's series expansion of a function which are infinitely
differentiable.
Theorem
7.5
(a) TaylorŌĆÖs Series
Let f ( x) be a function infinitely
differentiable at x = a .
Then f ( x) can be expanded as a series, in an interval ( x ŌłÆ a, x + a) , of the form
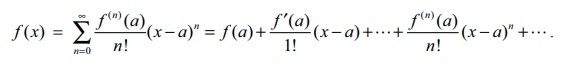
(b) MaclaurinŌĆÖs series
If a = 0 , the expansion takes the form
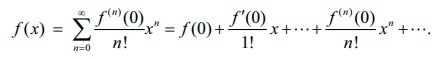
Proof
The
series expansion of f ( x) , in powers of ( x ŌłÆ a) , be given by
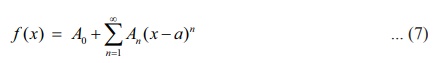
Substituting
x = a
gives A0 =
f (a) . Differentiation of (7) gives
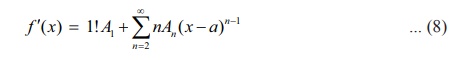
Substituting
x = a
gives A1 =
f ŌĆ▓(a)
. Differentiation of (8) gives
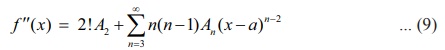
Substituting
x = a
gives A2 =
f ŌĆ▓ŌĆ▓(a)
/ 2!. Differentiation of (9) gives
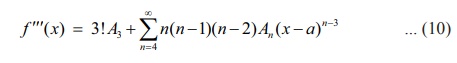
Differentiation
of (10) (k ŌłÆ
3) times gives
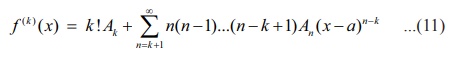
Substituting x = a gives
Ak = f (k)(a) / k!
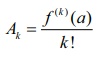
which completes the proof of the
theorem.
In order
to expand a function around a point say x
=
a , equivalently in powers of ( x ŌłÆ a)
we need to differentiate the given function as many times as the required
powers and evaluate at x =
a . This will give the value for the
coefficients of the required powers of ( x
ŌłÆ
a) .
Example 7.30
Expand
log(1+
x) as a MaclaurinŌĆÖs series upto 4
non-zero terms for ŌĆō1 < x Ōēż 1.
Solution
Let f (x) = log(1+ x) , then the Maclaurin series
of f (x) is f (x) = 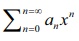 , where,
, where, 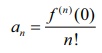 various derivatives of
the function f (x) evaluated at x = 0 are given below:
various derivatives of
the function f (x) evaluated at x = 0 are given below:

Substituting
the values and on simplification we get the required expansion of the function
given by,
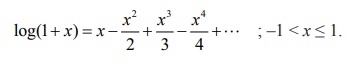
Example 7.31
Expand
tan x in ascending powers of x upto 5th power for ŌĆō ŽĆ/2 < x < ŽĆ/2.
Solution
Let f (x)
=
tan x . Then the Mclaurin series of f ( x)
is
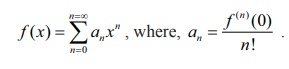
Various
derivatives of the function f ( x) evaluated at x = 0 are given below:
Now,
f
ŌĆ▓(x) = d/dx (tan x ) = sec2(x)
fŌĆÖŌĆ▓(x) = d/dx
(sec2 ( x )) = 2 sec x Ōŗģ sec x Ōŗģ
tan x = 2 sec2x Ōŗģ tan x
f ŌĆ▓ŌĆ▓ŌĆ▓(x) = d/dx
(2sec2 ( x ). tan x) = 2 sec2(x ) Ōŗģ sec2x + tan x Ōŗģ 4 sec x Ōŗģ
sec x Ōŗģ tan x
= 2 sec4 x + 4 sec2 x
Ōŗģ tan2 x
f (iv)(x) = 8sec3 x Ōŗģ sec x Ōŗģ tan x + 4 sec2 x Ōŗģ 2 tan x Ōŗģ sec2
x + 8sec x Ōŗģ sec x Ōŗģ tan x Ōŗģ tan2
x
= 16 sec4
x tan x + 8sec2 x
Ōŗģ tan3 x
f(v)( x) = 16 sec4 x Ōŗģ sec2 x + 64 sec3 x Ōŗģ sec x Ōŗģ tan x Ōŗģ tan x + 8sec2 x
Ōŗģ 3 tan2 x Ōŗģ sec2 x +16 sec x Ōŗģ sec x Ōŗģ tan x Ōŗģ tan3 x
= 16 sec6 x + 88sec4 x
Ōŗģ tan2 x + 16 sec2 x Ōŗģ tan4 x .

Substituting
the values and on simplification we get the required expansion of the function
as
tan x = x + 1/3 x3 + 2/15 x5 + .. ŌĆ” ; ŌłÆ ŽĆ/2 < x < ŽĆ/2
Example 7.32
Write
the Taylor series expansion of 1/ x about
x = 2 by finding the first three
non-zero terms.
Solution
Let f (x)
= 1/x, then the Taylor series of f (
x) is
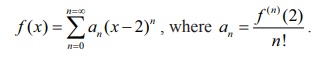
Various
derivatives of the function f (
x) evaluated at x = 2
are given below.
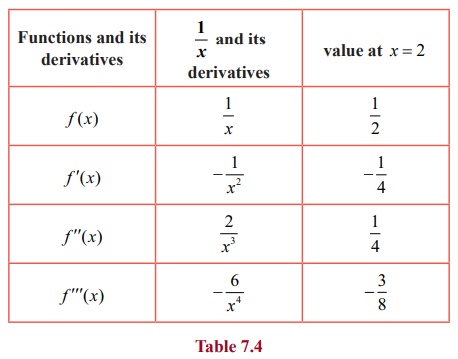
Substituting
these values, we get the required expansion of the function as
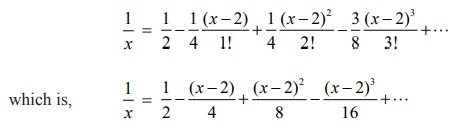
Related Topics