Equations of Tangent and Normal

Equations of Tangent and Normal

According to Leibniz, tangent is the line through a pair of very close points on the curve.

Definition 7.1

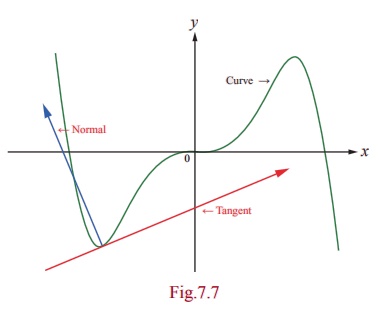
The tangent line (or simply tangent) to a plane curve at a given point is the straight line that just touches the curve at that point.

Definition 7.2

The normal at a point on the curve is the straight line which is perpendicular to the tangent at that point.

The tangent and the normal of a curve at a point are illustrated in Fig. 7.7.

Consider the given curve y = f ( x) .

The equation of the tangent to the curve at the point, say (a , b) , is given by

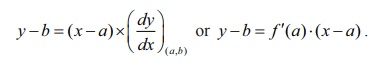
In order to get the equation of the normal to the same curve at the same point, we observe that normal is perpendicular to the tangent at the point. Therefore, the slope of the normal at (a , b) is the negative of the reciprocal of the slope of the tangent which is −( 1 / dy/ dx)_{( a , b)}. 

Hence, the equation of the normal is ,

Remark

(i) If the tangent to a curve is horizontal at a point, then the derivative at that point is 0. Hence, at that point ( x₁ , y₁ ) the equation of the tangent is y = y₁ and equation of the normal is x = x₁ .

(ii) If the tangent to a curve is vertical at a point, then the derivative exists and infinite ( ∞) at the point. Hence, at that point ( x₁ , y₁ ) the equation of the tangent is x = x₁ and the equation of the normal is y = y₁ .

Example 7.11

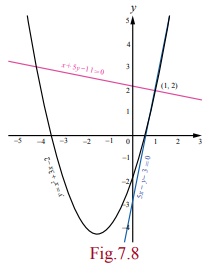
Find the equations of tangent and normal to the curve y = x² + 3x − 2 at the point (1, 2)

Solution

We have, dy/dx = 2x + 3 . Hence at (1, 2), dy/dx = 5 .

Therefore, the required equation of tangent is

( y − 2) = 5(x − 1) ⇒ 5x − y − 3 = 0 .

The slope of the normal at the point ( 1, 2) is – 1/5.

Therefore, the required equation of normal is

 ( y − 2) = − 1/5 (x −1) ⇒ x + 5 y − 11 = 0 .

Example 7.12

Find the points on the curve y = x³ − 3x² + x − 2 at which the tangent is parallel to the line y = x .

Solution

The slope of the line y = x is 1. The tangent to the given curve will be parallel to the line, if the slope of the tangent to the curve at a point is also 1. Hence,

dy/dx = 3x² − 6x +1 = 1

which gives 3x² − 6x = 0 .

Hence, x = 0 and x = 2.

Therefore, at (0, –2) and (2, –4) the tangent is parallel to the line y = x .

Example 7.13

Find the equation of the tangent and normal at any point to the Lissajous curve given by x = 2 cos 3t and y = 3 sin 2t, t ∈ R.

Solution

Observe that the given curve is neither a circle nor an ellipse. For your reference the curve is shown in Fig. 7.9.

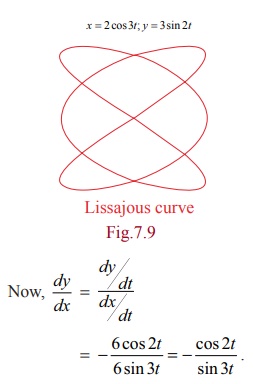
Therefore, the tangent at any point is

 y − 3sin 2t = − cos 2t/ sin 3t  (x − 2 cos 3t)

That is, x cos 2t + y sin 3t = 3sin 2t sin 3t + 2 cos 2t cos 3t .

The slope of the normal is the negative of the reciprocal of the tangent which in this case is sin3t / cos2t . Hence, the equation of the normal is

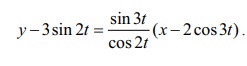
y − 3sin 2t = [sin 3t / cos 2t] (x − 2 cos 3t) .

That is, x sin 3t − y cos 2t = 2 sin 3t cos 3t − 3sin 2t cos 2t = sin 6t − 3/2 sin 4t .