Applications in Optimization

Applications in Optimization

Optimization is a process of finding an extreme value (either maximum or minimum) under certain conditions.

A procedure for solving for an extremum or optimization problems.

Step 1 : Draw an appropriate figure and label the quantities relevant to the problem.

Step 2 : Find a experssion for the quantity to be maximized or minimized.

Step 3 : Using the given conditions of the problem, the quantity to be extremized .

Step 4 : Determine the interval of possible values for this variable from the conditions given in the problem.

Step 5 : Using the techniques of extremum (absolute extrimum, first derivative test or second derivative test) obtain the maximum or minimum.

Example 7.62

We have a 12 unit square piece of thin material and want to make an open box by cutting small squares from the corners of our material and folding the sides up. The question is, which cut produces the box of maximum volume?

Solution

Let x = length of the cut on each side of the little squares.

 V = the volume of the folded box.

The length of the base after two cuts along each edge of size x is 12 − 2x . The depth of the box after folding is x , so the volume is V = x × (12 − 2x)² . Note that, when x = 0 or 6 , the volume is zero and hence there cannot be a box. Therefore the problem is to maximize, V = x × (12 − 2x )² , x ∈(0, 6).

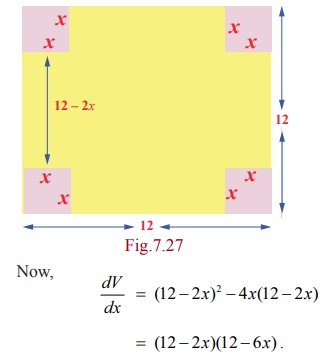
Now, dV / dx = (12 − 2x)² − 4x(12 − 2x)

 = (12 − 2x )(12 − 6x).

dV / dx = 0 gives the stationary numbers x = 2, 6 . Since  6∉(0,6) the only stationary number is at x = 2 ∈(0, 6) . Further, dV  / dx  changes its sign from postive to negative when passing through x = 2 . Therefore at x = 2 the volume V is local maximum. The local maximum volume value is V = 128 units. Hence the maximum cut can only be 2 units.

Example 7.63

Find the points on the unit circle x² + y² = 1 nearest and farthest from (1,1) .

Solution

The distance from the point (1,1) to any point ( x , y) is d = √{(x −1)² + ( y −1)²} . Instead of extremising d, for convenience we extremise D = d² = (x − 1)² + (y −1)², subject to the condition x² + y² =1. Now, dD/dx = 2(x − 1) + 2( y −1) × dy/dx , where the dy/dx will be computed by differentiating x² + y² = 1 with respect to x . Therefore, we get 2x + 2y dy/dx = 0 which gives us dy/dx = − x/y .

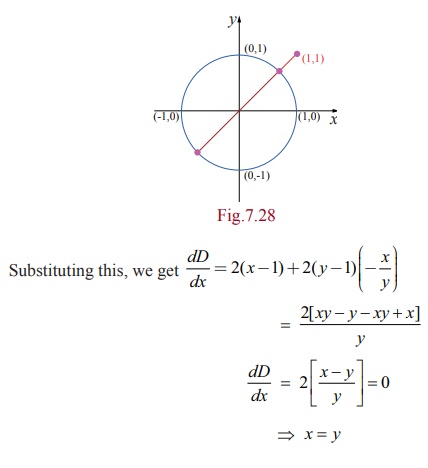
Since ( x , y) lie on the circle x² + y² =1, we get 2x² =1 which gives x = ± 1/√2 . Hence the points at which the extremum distance occur are, (1/√2, 1/√2), (-1/√2, -1/√2).

To find the extrema, we apply second derivative test. So,

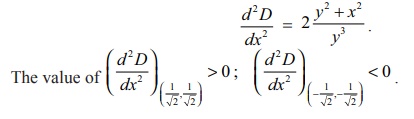
This implies the nearest and farthest points are (1/√2, 1/√2) and (-1/√2, -1/√2) respectively.

Therefore, the nearest and the farthest distances are respectively √2 - 1 and √2 + 1.

Example 7.64

A steel plant is capable of producing x tonnes per day of a low-grade steel and y tonnes per day of a high-grade steel, where y = 40−5x  / 10-x or [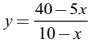]. If the fixed market price of low-grade steel is half that of high-grade steel, then what should be optimal productions in low-grade steel and high-grade steel in order to have maximum receipts.

Solution

Let the price of low-grade steel be ₹p per tonne. Then the price of high-grade steel is ₹2p per tonne.

The total receipt per day is given by R = px + 2py = px + 2p[40−5x  / 10-x]. Hence the problem is to maximise R . Now, simplifying and differentiating R with respect to x , we get

and hence R will be maximum. If x = 10-2√5 then y = 5 − √5 . Therefore the steel plant must produce low-grade and high-grade steels respectively in tonnes per day are

10-2√5 and 5 − √5.

Example 7.65

Prove that among all the rectangles of the given area square has the least perimeter.

Solution

Let x , y be the sides of the rectangle. Hence the area of the rectangle is xy = k (given). The perimeter of the rectangle P is 2(x + y) . So the problem is to minimize 2(x + y) suject to the condition xy = k . Let P (x) = 2 (x + k/x).

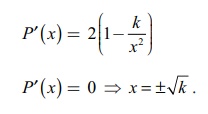
 P ′(x) = 0 ⇒ x = ±√k.

As x, y are sides of the rectangle, x = √k is a critical number.

Now, P ′′ (x) = 4k/ x³ and P ′′ ( √k ) > 0 ⇒ P ( x) has its minimum value at x = √k .

Substituting x = √k in xy = k we get y = √k . Therefore the minimum perimeter rectangle of a given area is a square.