Indeterminate Forms

Indeterminate Forms

In this section, we shall discuss various “indeterminate forms” and methods of evaluating the limits when we come across them.

A Limit Process

While computing the limits

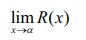
lim _x→α R(x)

of certain functions R( x) , we may come across the following situations like,

We say that they have the form of a number. But values cannot be assigned to them in a way that is consistent with the usual rules of addition and mutiplication of numbers. We call these expressions indeterminate forms. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function.

John (Johann) Bernoulli discovered a rule using derivatives to compute the limits of fractions whose numerators and denominators both approach zero or ∞. The rule is known today as l’Hôpital’s Rule (pronounced as Lho pi tal Rule), named after Guillaume de l’Hospital’s, a French nobleman who wrote the earliest introductory differential calculus text, where the rule first appeared in print.

The l’Hôpital’s Rule

Suppose f ( x) and g ( x) are differentiable functions and g(x′) ≠ 0 with

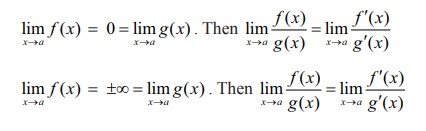
Indeterminate forms  0/0, ∞/∞, 0×∞, ∞-∞

Example 7.33

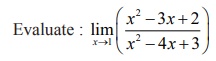
Solution

If we put directly x = 1 we observe that the given function is in an indeterminate form 0/0. As the numerator and the denominator functions are polynomials of degree 2 they both are differentiable. Hence, by an application of the l’Hôpital Rule, we get

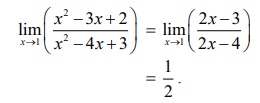
Note that this limit may also be evaluated through the factorization of the numerator and denominator as

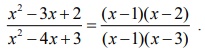
Example 7.34

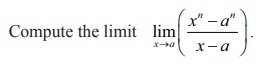
Solution

If we put directly x =a we observe that the given function is in an indeterminate form 0/0 . As the numerator and the denominator functions are polynomials they both are differentiable.

Hence by an application of the l’Hôpital Rule we get,

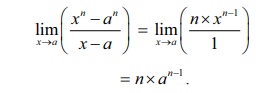
Example 7.35

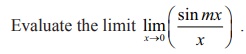
Solution

If we directly substitute x = 0 we get an indeterminate form  0/0 and hence we apply the l’Hôpital’s rule to evaluate the limit as,

The next example tells that the limit does not exist.

Example 7.36

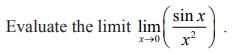
Solution

If we directly substitute x = 0 we get an indeterminate form 0/0 and hence we apply the l’Hôpital’s rule to evaluate the limit as,

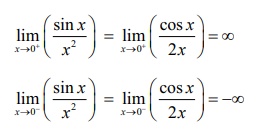
As the left limit and the right limit are not the same we conclude that the limit does not exist.

Remark

One may be tempted to use the l’Hôpital’s rule once again in

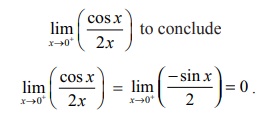
which is not true because it was not an indeterminate form.

Example 7.37

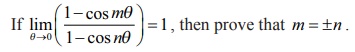
Solution

As this is an indeterminate form (0/0), using the l’Hôpital’s Rule

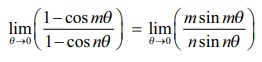
Now using the example 7.35, we have

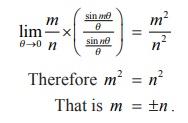
Example 7.38

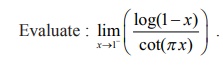
Solution

This is an indeterminate form ∞/∞ and hence we use the l’Hôpital’s Rule to evaluate the limit.

Example 7.39

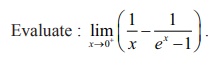
Solution

This is an indeterminate of the form ∞ − ∞ . To evaluate this limit we first simplify and bring it in the form (0/0) and applying the l’Hôpital Rule, we get

Example 7.40

Evaluate : 

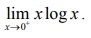
Solution

This is an indeterminate of the form (0 × ∞) . To evaluate this limit, we first simplify and bring it to the form (∞/∞) and apply l’Hôpital Rule. Thus, we get

Example 7.41

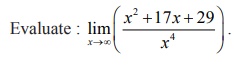
Solution

This is an indeterminate of the form (∞/∞) . To evaluate this limit, we apply l’Hôpital Rule.

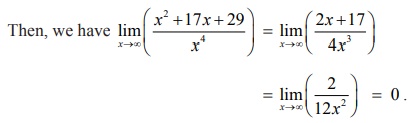
Example 7.42

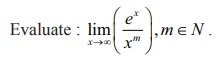
Solution

This is an indeterminate of the form (∞/∞).

To evaluate this limit, we apply l’Hôpital Rule m times.

Thus, we have

lim_x→∞ e^x/x^m  = lim_x→∞ e^x/m!

= ∞ .

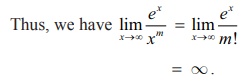
Indeterminate forms 0⁰,1^∞ and ∞⁰

In order to evaluate the indeterminate forms like this, we shall first state the theorem on the limit of a composite function.

Theorem 7.6

Let lim_x→α g ( x) exist and let it be L and let f (x) be a continuous function at x = L . Then,

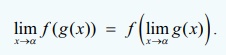
The evaluation procedure for evaluating the limits

(1) Let A = lim_x→α g(x) . Then taking logarithm, with the assumption that A > 0 to ensure the continuity of the logarithm function, we get log A = lim_x→α log(g(x)) . Therefore using the above theorem with f (x) = log x we have the limit

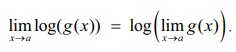
(2) We have the limit lim _x→α log(g ( x)) into either (0/0) or (∞/∞) form evaluate it using l’Hôpital Rule.

(3) Let that evaluated limit be say α . Then the required limit is e^α .

Example 7.43

Using the l’Hôpital Rule, prove that lim_x→α (1+ x )^1/x = e .

Solution

This is an indeterminate of the form 1^∞ . Let g ( x) = (1+ x)^1/x. Taking the logarithm, we get