Mean Value Theorem

Mean Value Theorem

Mean value theorem establishes the existence of a point, in between two points, at which the tangent to the curve is parallel to the secant joining those two points of the curve. We start this section with the statement of the intermediate value theorem as follows :

Theorem 7.1 (Intermediate value theorem)

If f is continuous on a closed interval [a , b] , and c is any number between f (a) and f (b) inclusive, then there is at least one number x in the closed interval [a , b] , such that f ( x) = c .

Rolle’s Theorem

Theorem 7.2 (Rolle’s Theorem)

Let f ( x) be continuous on a closed interval [a , b] and differentiable on the open interval (a , b)

If f (a) = f (b) , then there is at least one point c ∈ (a, b) where f’(c) =0.

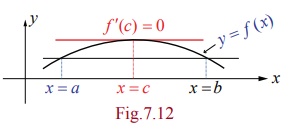
Geometrically this means that if the tangent is moving along the curve starting at x = a towards as in Fig 7.2 x = b then there exists a c ∈ ( a, b) at which the tangent is parallel to the x -axis. 

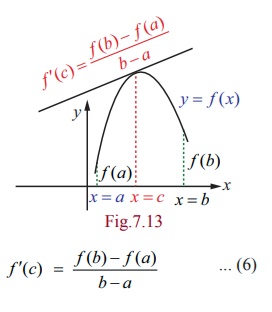
Lagrange’s Mean Value Theorem

Theorem 7.3

Let f (x) be continuous in a closed interval [a, b] and  differentiable in the open interval (a , b) (where f (a), f (b) are not necessarily equal). Then there exist at least one point c ∈( a , b) such that, 

 f ′(c) = f (b) − f (a) / b − a ... (6)

Remark

If f (a) = f (b) then Lagrange’s Mean Value Theorem gives the Rolle’s theorem. It is also known as rotated Rolle’s Theorem.

Remark

A physical meaning of the above theorem is the number f (b) − f (a) / b − a = 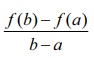 can be  thought of as the average rate of change in f ( x) over (a, b) and f (c) as an instantaneous change.

A geometrical meaning of the Lagrange’s mean value theorem is that the instantaneous rate of change at some interior point is equal to the average rate of change over the entire interval. This is illustrated as follows :

If a car accelerating from zero takes just 8 seconds to travel 200 m, its average velocity for the 8 second interval is 200/8 = 25 m/s. The Mean Value Theorem says that at some point during the travel the speedometer must read exactly 90 km/h which is equal to 25 m/s.

Theorem 7.4

If f ( x) is continuous in closed interval [a , b] and differentiable in open interval (a , b) and if f ′( x) > 0, ∀x ∈ (a, b) , then for, x₁ , x₂ ∈[a , b] , such that x₁ < x₂ we have, f (x₁ ) < f (x₂ ) .

Proof

By the mean value theorem, there exists a c ∈ ( x₁ , x₂ ) ⊂ (a, b) such that,

 f (x₂ ) − f (x₁)  /  x₂ − x₁ = f ′(c)

Since f ′(c) > 0 , and x₂ − x₁ > 0 we have f (x₂) – f (x₁) > 0.

We conclude that, whenever x₁ < x₂ , we have f (x₁ ) < f (x₂ ) .

Remark

If f ′( x) < 0, ∀x ∈ (a, b) , then for, x₁ , x₂ ∈ [a, b] , such that x₁ < x₂ we have, f (x₁ ) > f (x₂ ) .

The proof is similar.