Exercise 7.7: Applications of Second Derivative

EXERCISE 7.7

1. Find intervals of concavity and points of inflexion for the following functions:

(i) f (x) = x ( x âˆ’ 4)3

(ii) f (x) = sin x + cos x, 0 < x < 2Ï€

(iii) f (x) = 1/2 ( ex âˆ’ e−x )

2. Find the local extrema for the following functions using second derivative test :

(i) f (x) = −3x5 + 5x3

(ii) f (x) = x log x

(iii) f (x) = x2 e−2x

3. For the function f (x) = 4x3 + 3x2 âˆ’ 6x +1 find the intervals of monotonicity, local extrema, intervals of concavity and points of inflection.

Answers:

(1) (i) concave upwards on ( −∞, 2) and ( 4, ∞) . Concave downwards on ( 2, 4)

Points of inflection ( 2, −16) and ( 4, 0)

 (ii) concave upwards on . Concave downwards on 

Points of inflection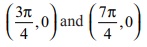 

(iii) concave upwards on ( 0, ∞). Concave downward on ( −∞, 0)  Points of inflection ( 0, 0)

(2) (i) local minimum = −2 ; local maximum = 2 (ii) local minimum = − 1/e  (iii) local minimum = 0 ; local maximum = 1/e2

(3) strictly increasing on (−∞, −1) and (1/2 , ∞) . strictly increasing on (−1, 1/2) local maximum = 6 , local minimum = − 3/4  concave downwards on (−∞, −1/4) ; concave upwards on (− 1/4, ∞) .  point of inflection (− 1/4, 21 /8)