Applications of Differential Calculus | Mathematics - Applications of Second Derivative | 12th Maths : UNIT 7 : Applications of Differential Calculus
Chapter: 12th Maths : UNIT 7 : Applications of Differential Calculus
Applications of Second Derivative
Applications of Second
Derivative
Second
derivative of a function is used to determine the concavity, convexity, the
points of inflection, and local extrema of functions.
Concavity, Convexity, and Points of Inflection
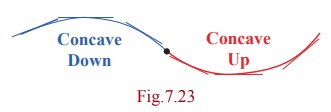
A graph
is said to be concave down (convex up) at a point if the tangent line lies
above the graph in the vicinity of the point. It is said to be concave up (convex
down) at a point if the tangent line to the graph at that point lies below the
graph in the vicinity of the point. This may be easily observed from the
adjoining graph.
Definition 7.8
Let f ( x) be a function whose second derivative
exists in an open interval I = (a,
b) . Then the function f ( x)
is said to be
(i) If f ŌĆ▓( x)
is strictly increasing on I , then
the function is concave up on an open interval I
(ii) If f ŌĆ▓( x)
is strictly decreasing on I , then
the function is concave down on an open interval I.
Analytically,
given a differentiable function whose graph y
=
f ( x) , then the concavity is given by the following result.
Theorem 7.11 (Test of Concavity)
(i) If f ŌĆ▓ŌĆ▓(x) > 0 on an open interval I , then f ( x) is concave up on I .
(ii) If f ŌĆ▓ŌĆ▓(x) < 0 on an open interval I , then f ( x) is concave down on I .
Remark
(1) Any
local maximum of a convex upward function defined on the interval [a , b]
is also its absolute maximum on this interval.
(2) Any
local minimum of a convex downward function defined on the interval [a , b]
is also its absolute minimum on this interval.
(3) There
is only one absolute maximum (and one absolute minimum) but there can be more
than one local maximum or minimum.
Points of Inflection
Definition 7.9
The
points where the graph of the function changes from ŌĆ£concave up to concave downŌĆØ or ŌĆ£concave down
to concave upŌĆØ are called the points of
inflection of f ( x) .
Theorem 7.12 (Test for Points of Inflection)
(i) If f ŌĆ▓ŌĆ▓(c) exists and f ŌĆ▓ŌĆ▓(c) changes sign when
passing through x = c , then the point (c
, f (c)) is a point of inflection of the graph of f .
(ii) If f ŌĆ▓ŌĆ▓(c)
exists at the point of inflection, then f
ŌĆ▓ŌĆ▓(c) = 0 .
Remark
To
determine the position of points of inflexion on the curve y = f ( x) it is necessary to find the points
where f ŌĆ▓ŌĆ▓(
x) changes sign. For ŌĆśsmoothŌĆÖ curves
(no sharp corners), this may happen when either
(i) f ŌĆ▓ŌĆ▓(x) = 0
or
(ii) f ŌĆ▓ŌĆ▓(
x) does not exist at the point.
Remark
(1) It
is also possible that f ŌĆ▓ŌĆ▓(c) may not exist, but (c , f
(c)) could be a point of inflection.
For instance, f (x) = x1/3
at c = 0 .
(2) It
is possible that f ŌĆ▓ŌĆ▓(c) = 0 at a point but (c , f
(c)) need not be a point of inflection.
For instance, f (x) = x4
at c = 0 .
(3) A
point of inflection need not be a stationary point. For instance, if f (x)
=
sin x then, f ŌĆ▓ (x) = cos x and f ŌĆ▓ŌĆ▓(x) = ŌłÆ sin x and hence (ŽĆ, 0) is a point of inflection but not a stationary point
for f (x) .
Example 7.57
Determine
the intervals of concavity of the curve f
(x) = (x ŌłÆ1)3 Ōŗģ ( x ŌłÆ 5), x Ōłł ŌäØ and, points of inflection if any.
Solution
The
given function is a polynomial of degree 4. Now,
f ŌĆ▓(x) = (x ŌłÆ 1)3 + 3(x ŌłÆ 1)2 Ōŗģ (x ŌłÆ 5)
= 4(x ŌłÆ
1)2 Ōŗģ
(x ŌłÆ 4)
f ŌĆ▓ŌĆ▓ (x)= 4((x ŌłÆ 1)2
+ 2(x ŌłÆ 1) Ōŗģ (x ŌłÆ
4))
= 12(x ŌłÆ 1) Ōŗģ (x ŌłÆ 3)
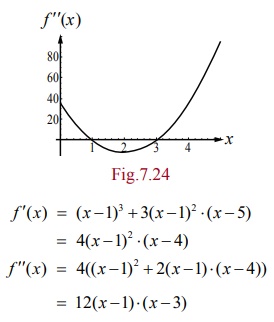
Now,
f ŌĆ▓ŌĆ▓( x) = 0 ŌćÆ x =1, x = 3 .
The
intervals of concavity are tabulated in Table 7.7.
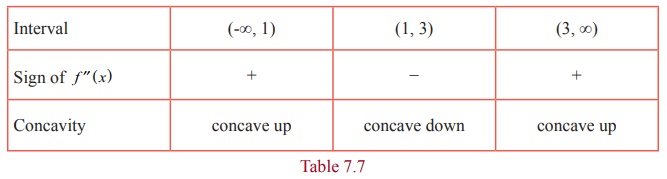
The
curve is concave upwards on (ŌłÆŌł×,1) and (3, Ōł×)
.
The
curve is concave downwards on (1, 3) .
As f ŌĆ▓ŌĆ▓(x)
changes its sign when it passes through x
= 1 and x = 3, (1, f (1)) = (1, 0) and (3, f (3)) = (3, ŌłÆ16) are points of inflection for the
graph y =
f ( x) . The sign change may be observed from the adjoining figure of
the curve f ŌĆ▓ŌĆ▓(
x) .
Example 7.58
Determine
the intervals of concavity of the curve y
=
3 +
sin x .
Solution
The
given function is a periodic function with period 2ŽĆ
and hence there will be stationary points and points of inflections in each
period interval. We have,
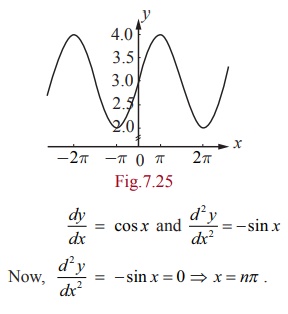
We now
consider an interval, (ŌłÆŽĆ
, ŽĆ ) by splitting into two sub intervals
(ŌłÆŽĆ , 0) and ( 0, ŽĆ) .
In the
interval (ŌłÆŽĆ , 0) , d2y/dx2 > 0 and hence the function is
concave upward.
In the
interval (0,ŽĆ ), d2y/dx2 < 0 and hence the function is concave
downward. Therefore (0, 3) is a point of inflection (see Fig. 7.25). The
general intervals need to be considered to discuss the concavity of the curve
are (nŽĆ
, (n +1)ŽĆ
) , where n is any integer which can
be discussed as before to conclude that (nŽĆ, 3) are also points of inflection.
Extrema using Second Derivative Test
The Second Derivative Test: The Second Derivative Test relates
the concepts of critical points, extreme
values, and concavity to give a very useful tool for determining whether a
critical point on the graph of a function is a relative minimum or maximum.
Theorem 7.13 (The Second Derivative Test)
Suppose
that c is a critical point at which f ŌĆ▓(c)
=
0 , that f ŌĆ▓(
x) exists in a neighborhood of c , and that f ŌĆ▓ŌĆ▓(c) exists. Then f has
a relative maximum value at c if f ŌĆ▓ŌĆ▓
(c) < 0 and a relative minimum value at c if f ŌĆ▓ŌĆ▓ (c ) > 0 . If f ŌĆ▓ŌĆ▓ (c) = 0 , the test is not
informative.
Example 7.59
Find the
local extremum of the function f (x) = x4
+
32x .
Solution
We have,
f ŌĆ▓(
x) = 4x3 + 32 = 0 gives x3 = ŌłÆ8
x = ŌłÆ2
and f ŌĆ▓ŌĆ▓( x) = 12x2.
As fŌĆ▓ŌĆ▓
(ŌłÆ2) > 0, the function has local minimum at x = ŌłÆ2 . The local minimum value is f (ŌłÆ 2) = ŌłÆ48 . Therefore, the extreme point is (ŌłÆ2, ŌłÆ48).
Example 7.60
Find the
local extrema of the function f (
x ) = 4x6 ŌłÆ6x4
.
Solution

Differentiating
with respect to x, we get
f ŌĆ▓( x) = 24x5 -24x3
= 24x3 ( x2 ŌłÆ1)
=
24x3 (
x +1)( x
ŌłÆ1)
f ŌĆ▓( x ) = 0 ŌćÆ x = ŌłÆ1,
0, 1. Hence the critical numbers are x
= ŌłÆ1,
0,1.
Now, f ŌĆ▓ŌĆ▓( x
)
=
120x4 ŌłÆ72x2 =
24x2 (5
x2 ŌłÆ3).
ŌćÆ f ŌĆ▓ŌĆ▓(ŌłÆ1) = 48 ,
f ŌĆ▓ŌĆ▓( 0) = 0 , f ŌĆ▓ŌĆ▓(1) = 48 .
As f ŌĆ▓ŌĆ▓(ŌłÆ1) and f ŌĆ▓ŌĆ▓(1) are positive by the second
derivative test, the function f (
x) has local minimum. But at x = 0, f ŌĆ▓ŌĆ▓(0)
=
0 . That is the second derivative test does not give any information about
local extrema at x =
0 . Therefore, we need to go back to the first derivative test. The intervals
of monotonicity is tabulated in Table 7.8.

By the
first derivative test f ( x) has local minimum at x = ŌłÆ1, its local minimum value is ŌłÆ2
. At x = 0 , the function f (
x) has local maximum at x = 0
, and its local maximum value is 0.
At x = 1, the function f ( x)
has local minimum at x =
1, and its local minimum value is ŌłÆ2 .
Remark
When the
second derivative vanishes, we have no information about extrema. We have used
the first derivative test to find out the extrema of the function!
Example 7.61
Find the
local maximum and minimum of the function x
2 y2 on the
line x + y
=
10 .
Solution
Let the
given function be written as f (x) = x2
(10 ŌłÆ
x)2. Now,
f (x) = x2 (100 ŌłÆ 20x
+ x2 ) = x4 ŌłÆ 20x3 +100x2
Therefore,
f ŌĆ▓(x) = 4x3 ŌłÆ 60x2
+ 200x = 4x(x2 ŌłÆ15x +
50)
f ŌĆ▓(x)
= 4x
(x2 ŌłÆ 15x + 50) = 0 ŌćÆ x = 0, 5, 10
and fŌĆ▓ŌĆ▓
(x) = 12x2 ŌłÆ 120x + 200
The
stationary numbers of f ( x)
are x = 0, 5, 10 at these
points the values of f ŌĆ▓ŌĆ▓ ( x)
are respectively 200, ŌłÆ100 and 200 . At x = 0 , it has local minimum and its
value is f (0) =
0 . At x =
5 , it has local maximum and its value is f
(5) =
625 . At x =
10 , it has local minimum and its value is f
(10) =
0 .
Related Topics