Applications of Differential Calculus | Mathematics - Sketching of Curves | 12th Maths : UNIT 7 : Applications of Differential Calculus
Chapter: 12th Maths : UNIT 7 : Applications of Differential Calculus
Sketching of Curves
Sketching of
Curves
When we
are sketching the graph of functions either by hand or through any graphing
software we cannot show the entire graph. Only a part of the graph can be
sketched. Hence a crucial question is which part of the curve we need to show
and how to decide that part. To decide on this we use the derivatives of
functions. We enlist few guidelines for determining a good viewing rectangle
for the graph of a function. They are :
(i) The
domain and the range of the function.
(ii) The
intercepts of the cure (if any).
(iii) Critical
points of the function.
(iv) Local
extrema of the function.
(v) Intervals
of concavity.
(vi) Asymptotes
of the curve (if exists)
(vii) Points
of inflexions (if any).
Example 7.69
Sketch
the curve y =
f (x ) = x2
ŌłÆ
x ŌłÆ 6 .
Solution
Factorising
the given function, we have
y= f (x ) = (x ŌłÆ 3)(x + 2) .

(1) The
domain of the given function f (x) is
the entire real line.
(2) Putting y = 0 we get x = ŌłÆ2, 3 . Therefore the x
-intercepts are (ŌłÆ2, 0) and (3, 0) putting x = 0 we get y = ŌłÆ6 .
Therefore the y -intercept is (0, ŌłÆ6)
.
(3) f ŌĆ▓(x) = 2x
ŌłÆ1 and hence the critical point of the
curve occurs at x =
1/2 .
(4) f ŌĆ▓ŌĆ▓(x) = 2
> 0, ŌłĆx . Therefore at x = 1/2 the curve has a local minimum which is f(1/2) = ŌłÆ 25/4.
(5) The
range of the function is y Ōēź ŌłÆ 25/4
(6) Since
f ŌĆ▓ŌĆ▓(x)
=
2 >
0, ŌłĆx the function is concave upward in
the entire real line.
(7) Since
f (x) = 2 ŌēĀ 0, ŌłĆx the curve has no points of
inflection.
(8) The
curve has no asymptotes.
The
rough sketch of the curve is shown on the right side.
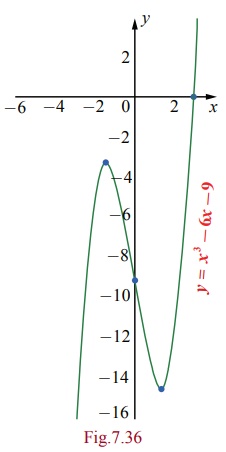
Example 7.70
Sketch
the curve y = f (x
) = x3 ŌłÆ 6x ŌłÆ 9 .
Solution
Factorising
the given function, we have
y
= f (x) = (x ŌłÆ 3)(x2 + 3x
+ 3) .
(1) The
domain and the range of the given function f
(x) are the entire real line.
(2) Putting y = 0 , we get the x = 3 . The other two roots are imaginary. Therefore, the x -intercept is (3, 0) . Putting x = 0, we get y = ŌłÆ9. Therefore, the y-intercept is (0, ŌłÆ9) .
(3) f ŌĆ▓
(x) = 3(x2 ŌłÆ 2) and hence the critical points of the curve occur
at x = ┬▒ ŌłÜ2 .
(4) f ŌĆ▓ŌĆ▓(x)
= 6x . Therefore at x = ŌłÜ2 the curve
has a local minimum because f ŌĆ▓ŌĆ▓ (ŌłÜ2)=6ŌłÜ2
> 0 . The local minimum is f (ŌłÜ2)=ŌłÆ4ŌłÜ2
ŌłÆ 9 . Similarly x = ŌłÆ ŌłÜ2 the curve
has a local maximum because f ŌĆ▓ŌĆ▓( ŌłÆ 2)=ŌłÆ6ŌłÜ2
< 0 . The local maximum is f (ŌłÆŌłÜ2)=4
ŌłÜ2ŌłÆ9.
(5) Since
f ŌĆ▓ŌĆ▓( x ) = 6x > 0, ŌłĆ x > 0 the function is
concave upward in the positive real line. As f ŌĆ▓ŌĆ▓( x ) = 6x < 0, ŌłĆ x < 0 the function is
concave downward in the negative real line.
(6) Since
f ŌĆ▓ŌĆ▓ ( x
)
=
0 at x = 0 and f ŌĆ▓ŌĆ▓( x) changes its
sign when passing through x =
0 . Therefore the point of inflection is ( 0, f ( 0)) = ( 0, ŌłÆ9) .
(7) The
curve has no asymptotes.
The
rough sketch of the curve is shown on the right side.
Example 7.71
Sketch
the curve y =
x2ŌłÆ3x / (xŌłÆ1).
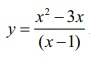
Solution
Factorising
the given function we have,
y = f (x) = x(xŌłÆ3) / (xŌłÆ1).
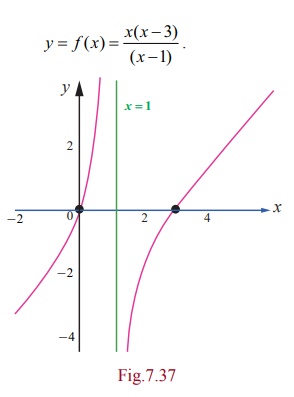
(1) The
domain and the range of f ( x) are respectively R \ {1} and the entire
real line.
(2) Putting
y = 0 we get the x = 0, 3 . Therefore the x
-intercept is (3, 0) . Putting x = 0
, we get y = 0 .
Therefore the curve passes through the origin.
(3) f ŌĆ▓(x)
=
x2ŌłÆ2x+3 / (x
ŌłÆ1)2 and hence
the critical point of the curve occurs at
x = 1 as f ŌĆ▓ (1) does not exist.
But x2 ŌłÆ 2x + 3 = 0 has no real solution. Hence
the only critical point occurs at x =
1 .
(4) x = 1 is not in the domain of the
function and f ŌĆ▓(x) ŌēĀ 0 ŌłĆ x Ōłł R\{1}, there is no local maximum or local minimum.
(5) f ŌĆ▓ŌĆ▓ (x) = ŌłÆ 4 / (x ŌłÆ1)3 ŌłĆx Ōłł \{1}. Therefore when x < 1, fŌĆ▓ŌĆ▓(x) > 0 the curve
is concave upwards in (ŌłÆŌł×,1) and when x >
1, fŌĆ▓ŌĆ▓ (x) < 0 the curve is concave downwards in (1, Ōł×) . Since x = 1 is not in the domain fŌĆ▓ŌĆ▓(x)
ŌēĀ 0 x Ōłł R\{1} there is no point of infection for f (x) .
(6) Since,
lim xŌåÆ1ŌłÆ x2ŌłÆ3x /
(xŌłÆ1) = +Ōł× and limxŌåÆ1+
x2ŌłÆ3x / (xŌłÆ1) = ŌłÆŌł× , x =1 is a vertical asymptote.
The
rough sketch is shown on the right side.
Example 7.72
Sketch the graph of the function y = 3x / x2 ŌłÆ1
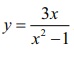
Solution
(1) The
domain of f ( x) is ŌäØ
\ {ŌłÆ1,1}.
(2)
Since f ( ŌłÆ x, ŌłÆ y ) = f ( x ,
y ) , the curve is symmetric about the origin.
(3) Putting
y = 0 , we get x = 0 . Hence the x
-intercept is ( 0, 0) .
(4) Putting
x = 0 , we get y = 0 . Hence the y -intercept is ( 0, 0) .
(5) To determine monotonicity, we find the first derivative as f ŌĆ▓( x ) = ŌłÆ3(x2+1) / ( x2ŌłÆ1)2.
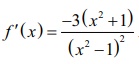
Hence, f ŌĆ▓ ( x
)
does not exist at x = ŌłÆ1,1.
Therefore, critical numbers are x = ŌłÆ1,1
.
The
intervals of monotonicity is tabulated in Table 7.9.
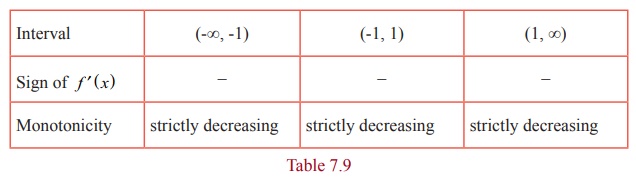
(6) Since
there is no sign change in f ŌĆ▓
(
x ) when passing through critical
numbers. There is no local extrema.
(7) To determine the concavity, we find the second derivative as f ŌĆ▓ŌĆ▓( x ) = 6x(x2+3) / (x2ŌłÆ1)3.
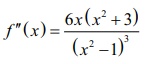
f ŌĆ▓ŌĆ▓( x ) = 0 ŌćÆ x = 0 and f ŌĆ▓ŌĆ▓ ( x ) does not exist at x = ŌłÆ1,1 .
The
intervals of concavity is tabulated in Table 7.10.
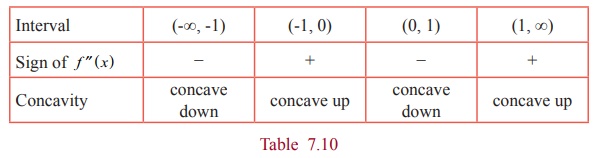
(8) As x = ŌłÆ1 and 1are not in the domain of f ( x
)
and at x =
0 ,the second derivative is zero and f ŌĆ▓ŌĆ▓( x ) changes its sign from positive to negative when passing
through x = 0 . .Therefore, the
point of inflection is ( 0, f ( 0)) = ( 0, 0) .
(9) 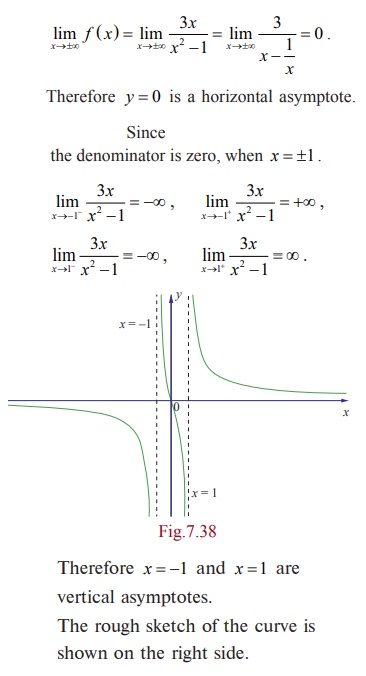
Therefore
x = ŌłÆ1 and x = 1 are vertical
asymptotes.
The
rough sketch of the curve is shown on the right side.
Related Topics