Exercise 7.3: Mean Value Theorem

EXERCISE 7.3

1. Explain why Rolle’s theorem is not applicable to the following functions in the respective intervals.

(i) f (x) = |1/x| , x âˆˆ[−1,1]

(ii) f (x) = tan x, x âˆˆ[0,Ï€ ]

(iii) f (x) = x âˆ’ 2 log x, x âˆˆ[2, 7]

2. Using the Rolle’s theorem, determine the values of x at which the tangent is parallel to the x -axis for the following functions :

(i) f (x) = x2 âˆ’ x, x âˆˆ[0,1]

(ii) f (x) = (x2 âˆ’ 2x) / (x + 2), x âˆˆ [ −1, 6]

(ii) f (x) = âˆšx â€“ x/3 , x âˆˆ[0, 9]

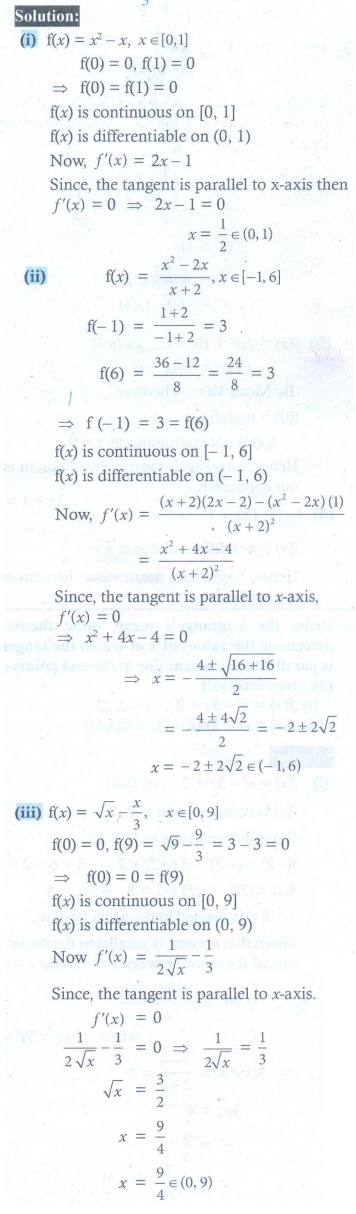
3. Explain why Lagrange’s mean value theorem is not applicable to the following functions in the respective intervals :

(i) f (x) = x +1 / x, x âˆˆ [ −1, 2]

(ii) f (x) = | 3x +1 |, x âˆˆ [ −1, 3]

4. Using the Lagrange’s mean value theorem determine the values of x at which the tangent is parallel to the secant line at the end points of the given interval:

(i) f ( x) = x3 âˆ’ 3x + 2, x âˆˆ[−2, 2]

(ii) f (x) = ( x âˆ’ 2)(x âˆ’ 7), x âˆˆ[3,11]

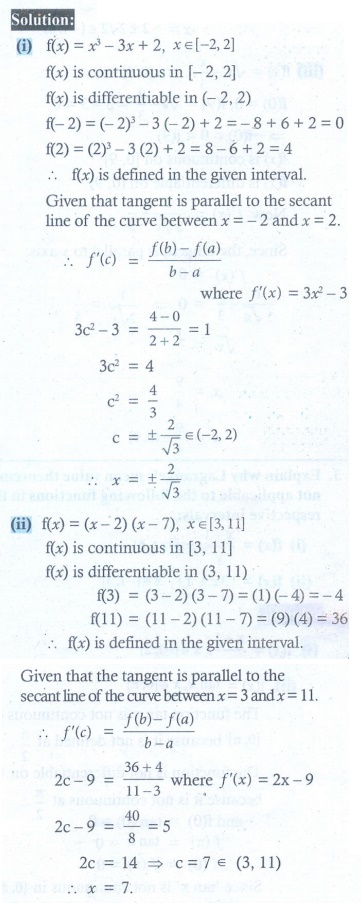
5. Show that the value in the conclusion of the mean value theorem for

(i) f (x) = 1/x on a closed interval of positive numbers [a, b] is √(ab)

(ii) f (x) = Ax2 + Bx + C on any interval [a, b] is (a +b) / 2 .

6. A race car driver is kilometer stone 20. If his speed never exceeds 150 km/hr, what is the maximum kilometer he can reach in the next two hours.

7. Suppose that for a function f ( x), f â€²( x) â‰¤ 1 for all 1 â‰¤ x â‰¤ 4 . Show that f (4) âˆ’ f (1) â‰¤ 3 .

8. Does there exist a differentiable function  f (x) such that f (0) = −1, f (2) = 4 and f’(x) â‰¤ 2 for all x . Justify your answer.

9. Show that there lies a point on the curve  f (x) = x ( x + 3)e-Ï€/2 , −3 ≤ x â‰¤ 0 where tangent drawn is parallel to the x -axis.

10. Using mean value theorem prove that for, a > 0, b > 0, | e−a âˆ’ e−b | < | a − b | .

Answers:

 (1) (i) not continuous at x = 0 (ii) not continuous at x = Ï€/2 (iii) Ï€ f ( 2) ≠ f (7)

(2) (i) 1/2 (ii) −2 + 2√2 (iii) 9/4

(3) (i) not continuous at x = 0 (ii) not differentiable at x = −1/3

(4) (i) ± 2/√3  (ii) 7

(6) 320 km

(8) No. Since f â€² ( x) cannot be 2.5 at any point in ( 0, 2) .