Derivative as slope

Derivative as slope

Slope or Gradient of a line: Let l be any given non vertical line as in the Fig. 7.1. Taking a finite horizontal line segment of any length with the starting point in the given line l and the vertical line segment starting from the end of the horizontal line to touch the given line. It can be observed that the ratio of the vertical length to the horizontal length is always a constant. This ratio is called the slope of the line l and it is denoted as m .

The slope can be used as a measure to determine the increasing or decreasing nature of a line. The line is said to be increasing or decreasing according as m > 0 or m < 0 respectively. When m = 0 , the value of y does not change. Recall that y = mx + c represents a straight line in the XY plane where m denotes the slope of the line.

Slope or Gradient of a curve: Let y = f ( x) be a given curve. The slope of the line joining the two distinct points ( x , f ( x)) and the point ( x + h, f ( x + h)) is

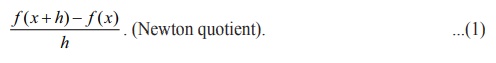
Taking the limit as h → 0 , we get

which is the slope of the curve at the point ( x , y) or ( x , f ( x)) .

Remark

If θ is the angle made by the tangent to the curve y = f ( x) at the Point ( x , y) , then the slope of the curve at ( x , y) is f’(x) = tan θ ,  where θ is measured in the anti-clockwise direction from the X -axis. Note that, f’(x) is also denoted by dy/dx and also called instantaneous rate of change. The average rate of change in an interval is calculated using Newton quotient.

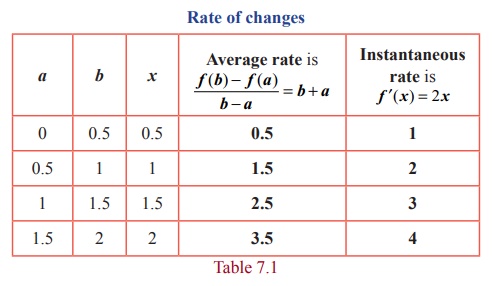
Example 7.1

For the function f (x) = x² , x ∈[0, 2] compute the average rate of changes in the subintervals [0, 0.5],[0.5,1],[1,1.5],[1.5, 2] and the instantaneous rate of changes at the points x = 0.5,1,1.5, 2 .

Solution

The average rate of change in an interval [a, b] is [ f (b) − f (a) ] / [b – a] whereas, the instantaneous rate of change at a point x is f ′( x) for the given function. They are respectively, b + a and 2x .

Rate of changes