Applications of Differential Calculus | Mathematics - Applications of First Derivative | 12th Maths : UNIT 7 : Applications of Differential Calculus
Chapter: 12th Maths : UNIT 7 : Applications of Differential Calculus
Applications of First Derivative
Applications of
First Derivative
Using
the first derivative we can test a function f
( x) for its monotonicity (increasing
or decreasing), focusing on a particular point in its domain and the local
extrema (maxima or minima) on a domain.
1. Monotonicity of functions
Monotonicity
of functions are its behaviour of increasing or decreasing.
Definition 7.4
A function f ( x) is said to be an increasing function
in an interval I
if a < b ⇒ f (a) ≤ f (b), ∀a, b ∈ I .
Definition 7.5
A function f ( x) is said to be a decreasing function
in an interval I
if a < b ⇒ f (a) ≥ f (b), ∀a, b ∈ I .
The
function f ( x) = x is an increasing function in the entire real line, whereas
the function f( x) = −x is a decreasing function in the
entire real line. In general, a given function may be increasing in some
interval and decreasing in some other interval, say for instance, the function f ( x)
=|
x | is decreasing in (−∞,
0] and is increasing in [ 0, ∞) . These functions are simple to
observe for their monotonicity. But given an arbitrary function how we
determine its monotonicity in an interval of a real line? That is where
following theorem (stated without proof) will be useful.
Theorem 7.7
If the function f (x) is
differentiable in an open interval ( a ,
b) then we say,
(1) if
d/dx( f (x)) ≥ 0, ∀ x ∈ (a , b) , ………(1)
then f (x) is
increasing in the interval ( a , b) ,
(2) if
d/dx ( f (x)) > 0, ∀ x ∈( a , b) , ……(2)
then f (x) is strictly
increasing in the interval ( a , b) .
The proof of the above can be observed from Theorem 7.3.
(3) f (x) is
decreasing in the interval ( a , b)
if
d/dx ( f (x)) ≤ 0, ∀x ∈( a , b) . ...(3)
(4) f (x) is strictly
decreasing in the interval (a , b) if
d/dx ( f (x)) < 0, ∀x ∈(a, b) . ... (4)
Remark
It is
very important to note the following fact. It
is false to say that if a differentiable
function f ( x) on I is strictly increasing on I , then f ′(x) > 0 for all x ∈ I . For instance, consider y = x3 , x ∈(−∞,
∞) . It is strictly increasing on (−∞,
∞) . To prove this, let a > b . Then we have to prove that f (a) >
f (b) . For this purpose, we have to prove a3 − b3
>
0 .
Now,
a3−
b3 = (a − b)(a2 + ab + b2 )
= (a − b) × 1/2 × (2a2 + 2ab + 2b2 )
= (a − b) × 1/2 × ((a+b)2 + a2 + b2 )
>0 since a − b >
0 and other terms inside the bracket are > 0 .
Hence it
is clear that the quadratic expression is always positive (it is equal to zero
only if a= b = 0 ,
which contradicts the condition a < b ). Therefore the function is y = x3 is
strictly increasing in (−∞, ∞)
. But f ′(x) = 3x2 which is equal to zero at x = 0 .
Definition 7.6
A stationary point ( x0
, f ( x0 )) of a differentiable function f ( x) is where f ′(x0 ) = 0 .
Definition 7.7
A critical point ( x0
, f ( x0 )) of a function f
( x) is where f ′(x0 ) = 0 or does not exist.
Note
We State
that if (x,y) is a Stationary point
or Critical Point of f where x from the domain of f is called Stationary number or
Critical number
Every
stationary point is a critical point however all critical points need not be
stationary points. As an example, the function f (x) =
| x −17 | has a critical point at (17, 0)
but (17, 0) is not a stationary point as the function has no derivative at x = 17 .
Example 7.46
Prove
that the function f (x) = x2
+
2 is strictly increasing in the interval (2, 7) and strictly decreasing in the
interval (−2, 0) .
Solution
We have,
f ′(
x) = 2x > 0, ∀x ∈(2, 7) and
f′( x) = 2x < 0, ∀x ∈ ( −2,
0)
and
hence the proof is completed.
Example 7.47
Prove
that the function f (x) = x2
−
2x − 3 is strictly increasing in ( 2, ∞)
.
Solution
Since f (x) = x2 − 2x − 3, f’(x) = 2x − 2 > 0 ∀ x ∈(2, ∞) . Hence f (x) is strictly increasing in (2, ∞).
2. Absolute maxima and minima
The
absolute maxima and absolute minima are referred to describing the largest and
smallest values of a function on an interval.
Definition 7.8
Let x0 be a
number in the domain D of a function f ( x)
. Then f (x0 ) is the absolute maximum value of f ( x)
on D , if f ( x0 ) ≥ f ( x) ∀x ∈ D and f (x0 ) is the absolute minimum
value of f ( x) on D if f ( x0 ) ≤ f ( x)∀x ∈ D .
In
general, there is no guarantee that a function will actually have an absolute
maximum or absolute minimum on a given interval. The following figures show
that a continuous function may or may not have absolute maxima or minima on an
infinite interval or on a finite open interval.
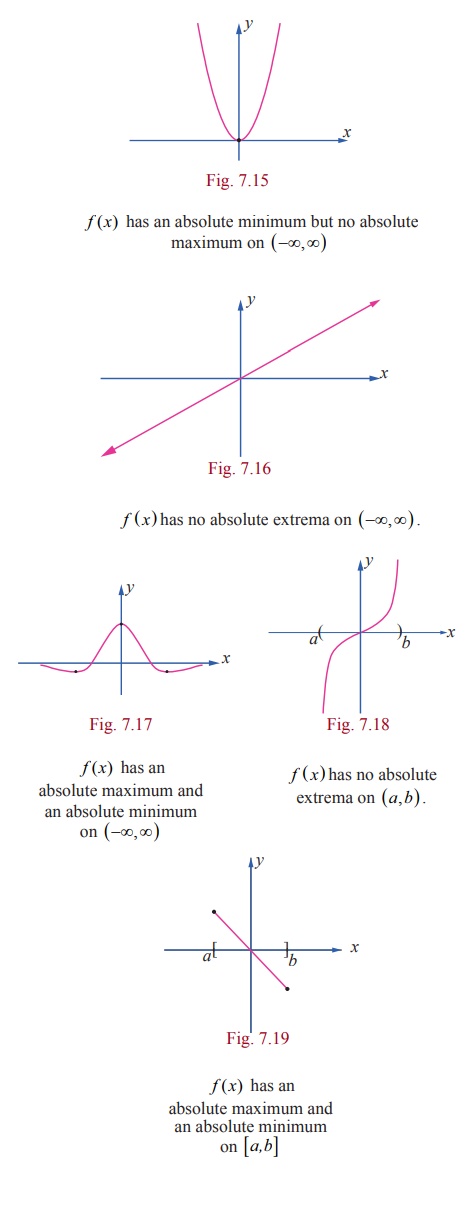
However,
the following theorem shows that a continuous function must have both an
absolute maximum and an absolute minimum on every closed interval.
Theorem 7.8 (Extreme Value Theorem)
If f ( x ) is continuous on a closed interval [ a ,
b] , then f has both an
absolute maximum and an absolute minimum on [ a , b] .
The
absolute extrema of f (
x ) occur either at the endpoints of
closed interval [ a
, b] or inside the open interval (
a , b) .If the absolute extrema occurs inside, then it must occur
at critical numbers of f (
x ) . Thus, we can use the following
procedure to find the absolute extrema of a continuous function on closed
interval [ a , b] .
A
procedure for finding the absolute extrema of a continuous function f ( x ) on closed interval [ a , b] .
Step 1 : Find the critical numbers of f ( x ) in ( a , b)
Step 2 : Evaluate f ( x ) at all
the critical numbers and at the endpoints
a and b
Step 3 : The largest and the smallest of the
values in step 2 is the absolute maximum and absolute minimum of f (
x ) respectively on the closed interval
[
a , b] .
Example 7.48
Find the
absolute maximum and absolute minimum values of the function f ( x
)
=
2x3 +
3x2 −12x on [ −3, 2]
Solution
Differentiating
the given function, we get
f′ (
x ) = 6x2 + 6x −12
= 6( x2
+
x − 2)
f′ (
x ) = 6( x + 2)( x −1)
Thus, f ′( x
)
=
0 ⇒ x
= −2,1∈ ( −3, 2) .
Therefore,
the critical numbers are x = −2,1 . Evaluating f ( x ) at the endpoints x = −3,
2 and at critical numbers x = −2,1 , we get f ( −3) = 9 , f ( 2) = 4 , f ( −2) = 20 and f (1) = −7 .
From
these values, the absolute maximum is 20 which occurs at x = −2
, and the absolute minimum is −7 which occurs at x = 1 .
Example 7.49
Find the
absolute extrema of the function f ( x ) = 3cos x on the closed interval [ 0, 2π ].
Solution
Differentiating
the given function, we get f ′ ( x ) = −3sin x .
Thus, f ′( x
)
=
0 ⇒ sin x = 0 ⇒
x = π
∈(
0, 2π ). Evaluating f ( x )
at the endpoints x =
0, 2π and at critical number x = π
, we get f (
0)
=
3 , f ( 2π
)
=
3 , and f (
π ) = −3 .
From
these values, the absolute maximum is 3 which occurs at x = 0, 2π
, and the absolute minimum is −3 which occurs at x = π
.
Relative Extrema on an Interval
A function
f ( x) is said to have a relative maximum at x0 , if there is an open interval containing x0 on which f (x0 ) is the largest value.
Similarly, f ( x) is said to have a
relative minimum at x0 , if
there is an open interval containing x0
on which f (x0 ) is the smallest value.
A
relative maximum need not be the largest value on the entire domain, while a
relative minimum need not be the smallest value on the entire domain.
Therefore, there may be more than one relative maximum or relative minimum on
the entire domain.
A
relative extrema of a function is the extreme values (maximum or minimum) of
the functions among all the evaluated values of f ( x), ∀x ∈ I
⊂ D
where I may be open or closed.
Usually the local extreme value of a function is attained at a critical point.
Note that, a function may have a critical point at x = c without having
a local extreme value there. For instance, both of the functions y = x3
and y =
x1/3 have critical points
at the origin, but neither function has a local extreme value at the origin.
Theorem 7.9 (Fermat)
If f (x) has a
relative extrema at x = c then c is a
critical number. Invariably there will be critical numbers of the function
obtained as solutions of the equation f ′(x)
= 0 or as values of x at which f ′( x) does not exist.
Extrema using First Derivative Test
After we
have determined the intervals on which a function is increasing or decreasing,
it is not difficult to locate the relative extrema of the function. The
location or points at which the relative extrema occurs for a given function f ( x)
can be observed through the graph y =
f ( x) . However to find the exact point and the value of the extrema
of functions we need to use certain test on functions. One such test is the
first derivative test, which is stated in the following theorem.
Theorem 7.10 (First Derivative Test)
Let (c , f (c)) be a critical point of function f ( x) that is continuous on an open interval I containing c .
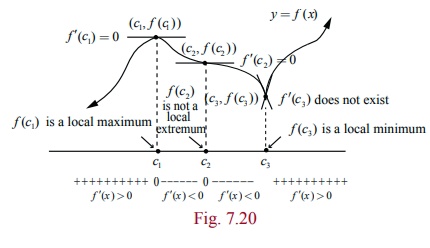
If f (
x) is differentiable on the interval, except possibly at c , then f (c) can be classified as follows:
(when
moving across the interval I from
left to right)
(i) If f ′( x) changes from negative to positive at c , then f ( x) has a local minimum f (c)
(ii) If f ′(
x) changes from positive to negative
at c , then f ( x) has a local
maximum f (c).
(iii) If
f ′( x) is positive on both sides of c
or negative on both sides of c , then
f (c) is neither a local minimum nor a local maximum.
Example 7.50
Find the
intervals of monotonicity and hence find the local extrema for the function f (x) = x 2 − 4x + 4
.
Solution
We have,
f (x) = (x − 2)2 , then
f’(x) = 2(x − 2) = 0 gives x = 2 .
The
intervals of monotonicity are (−∞, 2) and (2, ∞) . Since f’(x) < 0 , for x ∈(−∞, 2) the function f (x) is strictly decreasing on (−∞, 2)
. As f’(x) > 0 , for x ∈(2, ∞) the function f (x) is strictly increasing on (2, ∞) .
Because f’( x)
changes its sign from negative to positive when passing through x = 2 for the function f ( x)
, it has a local minimum at x =
2 . The local minimum value is f (2) = 0
.
Example 7.51
Find the
intervals of monotonicity and hence find the local extrema for the function f ( x ) = x2/3.
Solution
We have,
f (x) = x2/3 , then f ′
( x ) = 2/3 x−1/3 = 2 / 3x1/3
. f ′ (x) ≠ 0 ∀x
∈ ℝ and f ′ ( x ) does not exist
at x = 0 . Therefore, there are no stationary
points but there is a critical point at x
= 0 .
Because f ′ ( x
)
changes its sign from negative to positive when passing through x = 0
for the function f (
x ) , it has a local minimum at x = 0 .The local minimum value is f ( 0) = 0 . Note that here the local minimum occurs at a
critical point which is not a stationary point.
Example 7.52
Prove
that the function f (x) = x
−
sin x is increasing on the real line.
Also discuss for the existence of local extrema.
Solution
Solution
f’(x) = 1− cos x ≥ 0 and zero at the points x
= 2nπ , n ∈ Z and hence the function is increasing
on the real line.
Since
there is no sign change in f’(x) when passing through x = 2nπ
, n ∈ Z by the first derivative test there is no local extrema.
Example 7.53
Discuss
the monotonicity and local extrema of the function f (x)
= log(1 + x) – ( x/1+x)
, x > −1 and hence find the
domain where, log(1+ x) > x/1+x .
Solution
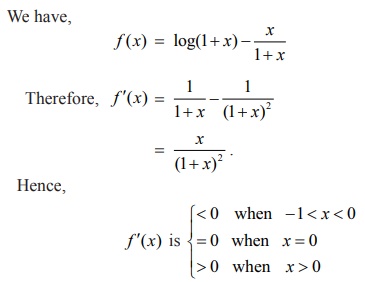
Therefore
f ( x) is strictly increasing for x
>
0 and strictly decreasing for x <
0 . Since f′(
x) changes from negative to positive
when passing through x =
0 , the first derivative test tells us there is a local minimum at x = 0 which is f (0) = 0 . Further, for x > 0
, f (x) > f (0) = 0 gives
log(1+ x) –
x/(1 + x) > 0 ⇒
log(1+ x) > x/(1 + x)
on (0, ∞) .
Example 7.54
Find the
intervals of monotonicity and local extrema of the function f (x)
=
x log x + 3x
Solution
The
given function is defined and is differentiable at all x ∈ (0, ∞)
.
f (x) = x log x + 3x .
Therefore
f ‘ (x) = log x +1+ 3 = 4 + log x .
The
stationary numbers are given by 4 + log x
= 0 .
That is x = e−4.
Hence
the intervals of monotonicity are (0, e−4 ) and (e−4 , ∞)
.
At x = e−5 ∈ (0, e−4), f′( e−5
) = −1 < 0 and hence in the interval (0, e−4 ) the function is
strictly decreasing.
At x = e−3 ∈(e−4 , ∞), f ′(e−3 ) = 1 > 0 and
hence strictly increasing in the interval (e−4 , ∞) . Since f’( x) changes from negative to positive
when passing through x = e−4
, the first derivative test tells us there is a local minimum at x = e−4 and it is f (e−4) = −e−4 .
Example 7.55
Find the
intervals of monotonicity and local extrema of the function f (x)
= 1 / 1+
x2
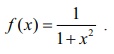
Solution
The given function is defined and is differentiable at all x ∈ ( −∞ , ∞) . As
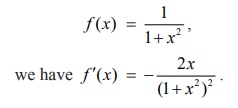
The
stationary numbers are given by − 2x / (1+ x2)2 =
0 that is x = 0 .
Hence
the intervals of monotonicity are (−∞, 0) and (0, ∞) .
On the
interval (−∞, 0) the function strictly increases because f (x) > 0 in that
interval.
The
function f (x) strictly decreases in
the interval (0, ∞) because f ‘ (x) <
0 in the interval. Since f ‘ (x) changes
from positive to negative when passing through
x = 0 , the first derivative
test tells us there is local maximum at x
= 0 and the local maximum value is f (0)
= 1.
Example 7.56
Find the
intervals of monotonicity and local extrema of the function f (x) = x / 1+ x2.
Solution
The
given function is defined and differentiable at all x ∈
( −∞ , ∞) , As
f (x) = x / 1+ x2,
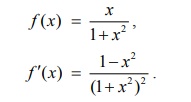
The
stationary numbers are given by 1− x2
= 0 that is x = ±1.
Hence
the intervals of monotonicity are (−∞,− 1), (−1,1) and (1, ∞) .
Therefore,
f (x) strictly increasing on (−∞,−1) and
(1, ∞) , strictly decreasing on (-1,1).
Since f (x) changes from negative to positive when
passing through x = −1 , the first
derivative test tells us there is a local minimum at x = −1 and the local minimum value is f (−1) = − 1/2. As f ‘(x)
changes from positive to negative when passing through x =1, the first derivative test tells us there is a local maximum
at x =1 and the local maximum value is
f (1)= 1/2.
Related Topics