Exercise 7.2 : Equations of Tangent and Normal, Angle between two curves

EXERCISE 7.2

1. Find the slope of the tangent to the following curves at the respective given points.

(i) y = x4 + 2x2 − x at x = 1

(ii) x = a cos3 t , y = b sin3 t at t = π/2.

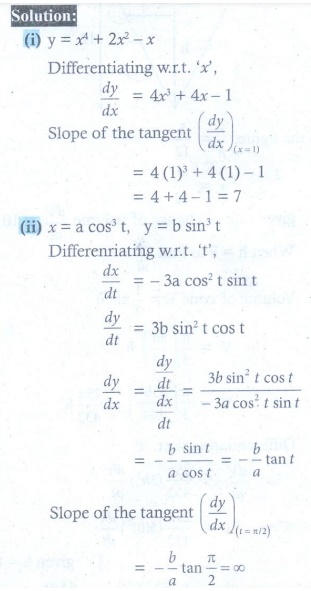
2. Find the point on the curve y = x2 − 5x + 4 at which the tangent is parallel to the line 3x + y = 7 .

3. Find the points on the curve y = x3 − 6x2 + x + 3 where the normal is parallel to the line x + y = 1729 .

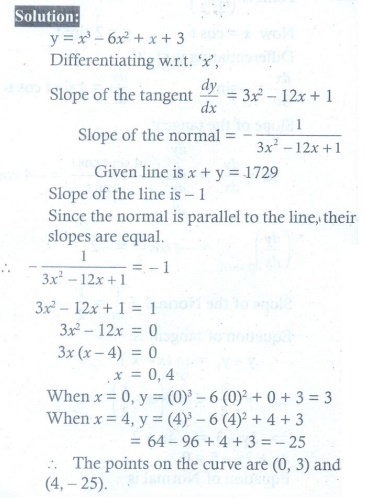
4. Find the points on the curve y2 − 4xy = x2 + 5 for which the tangent is horizontal.

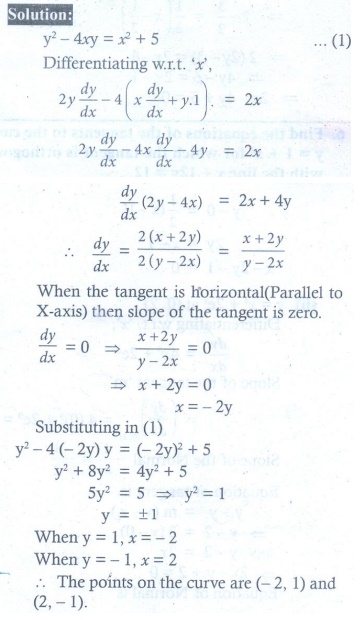
5. Find the tangent and normal to the following curves at the given points on the curve.

(i) y = x2 – x4 at (1, 0)  

(ii) y = x4 + 2ex  at ( 0, 2)

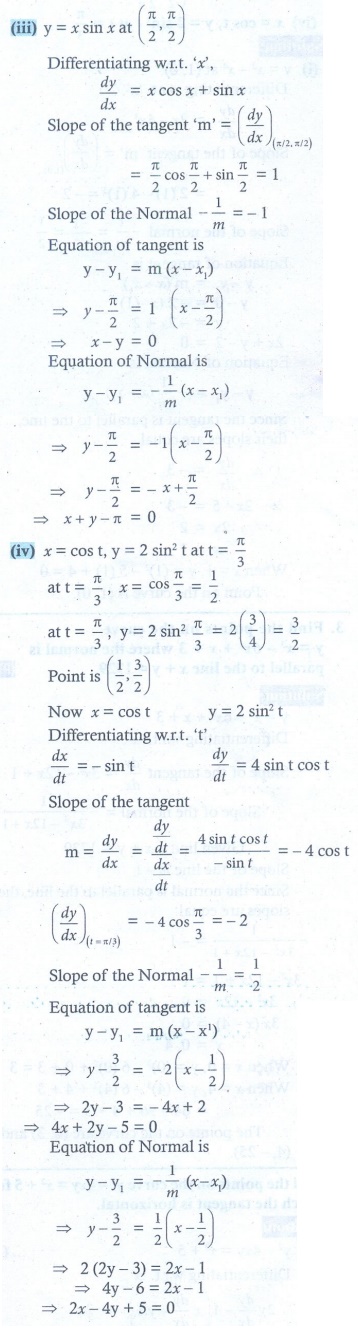
6. Find the equations of the tangents to the curve y = 1+ x3 for which the tangent is orthogonal with the line x + 12 y = 12 .

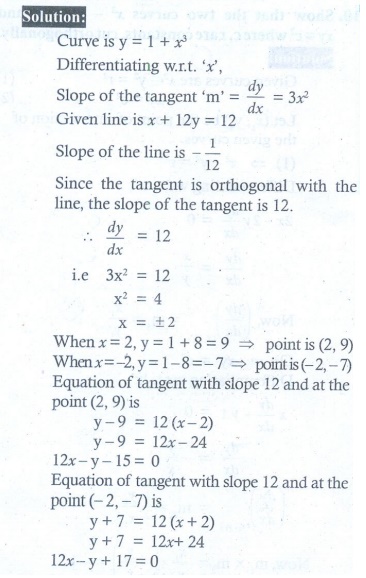
7. Find the equations of the tangents to the curve y = x+1 / x-1 which are parallel to the line x + 2 y = 6 .

8. Find the equation of tangent and normal to the curve given by x = 7 cos t and y = 2sin t, t ∈ ℝ at any point on the curve.

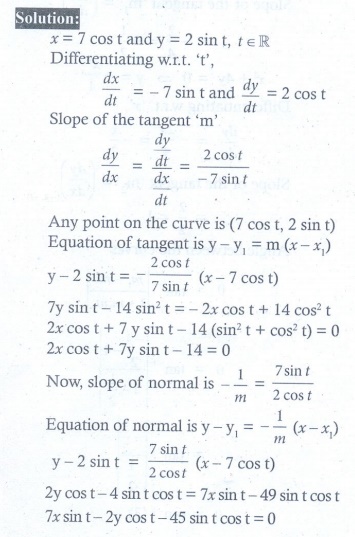
9. Find the angle between the rectangular hyperbola xy = 2 and the parabola x2 + 4y = 0.

10. Show that the two curves x2 − y2 = r2 and xy = c2 where c , r are constants, cut orthogonally.

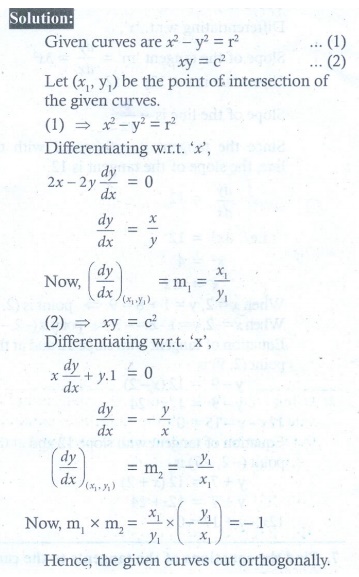
Answers:

(1) (i) 7 (ii) ∞

(2) (1, 0)

(3) ( 0, 3 and ( 4, − 25 )

(4) ( 2, −1) and (−2,1 )

(5) (i) 2x + y = 2 ; x − 2 y = 1 (ii) 2x − y = −2 ; x + 2 y = 4  (iii) x − y = 0 ; x + y = π (iv) 4x + 2 y = 5 ; 2x − 4 y = −5

(6) 12x − y = 15 ;12x − y = −17

(7) x + 2 y = 7 ; x + 2 y = −1

(8) (2 cos t ) x + (7 sin t ) y = 14 ; (7 sin t ) x − (2 cos t ) y = 45sin t cos t

(9) tan−1 (3)