Applications - Mean Value Theorem

Applications

Example 7.26

A truck travels on a toll road with a speed limit of 80 km/hr. The truck completes a 164 km journey in 2 hours. At the end of the toll road the trucker is issued with a speed violation notice. Justify this using the Mean Value Theorem.

Solution

Let f (t ) be the distance travelled by the trucker in 't ' hours. This is a continuous function in [0, 2] and differentiable in (0, 2) . Now, f (0) = 0 and f (2) = 164 . By an application of the Mean Value Theorem, there exists a time c such that,

f′(c) = 164 − 0 / 2-0 = 82 > 80 .

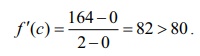
Therefore at some point of time, during the travel in 2 hours the trucker must have travelled with a speed more than 80 km/hr which justifies the issuance of a speed violation notice.

Example 7.27

Suppose f (x) is a differentiable function for all x with f (x) ≤ 29 and f (2) = 17 . What is the maximum value of f (7) ?

Solution

By the mean value theorem we have, there exists ' c ' ∈ (2, 7) such that,

 f (7) − f (2) / (7–2) = f ‘(c)  â‰¤ 29.

Hence, f (7) ≤ 5× 29 +17 = 162

Therefore, the maximum value of f (7) is 162 .

Example 7.28

Prove, using mean value theorem, that

| sin α − sin β | ≤ | α − β |, α , β ∈ .

Solution

Let f (x) = sin x which is a differentiable function in any open interval. Consider an interval [α , β ] . Applying the mean value theorem there exists c ∈(α , β ) such that,

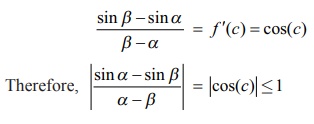
Hence, | sin α − sin β | ≤ | α − β | .

Remark

If we take β = 0 in the above problem, we get | sin α | ≤ | α | .

Example 7.29

A thermometer was taken from a freezer and placed in a boiling water. It took 22 seconds for the thermometer to raise from − 10°C to 100°C . Show that the rate of change of temperature at some time t is 5°C per second.

Solution

Let f (t ) be the temperature at time t. By the mean value theorem, we have

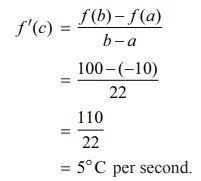
 = 5°C per second.

Hence the instantaneous rate of change of temperature at some time t is 5°C per second.