Rolle’s Theorem

Rolle’s Theorem

Theorem 7.2 (Rolle’s Theorem)

Let f ( x) be continuous on a closed interval [a , b] and differentiable on the open interval (a , b)

If f (a) = f (b) , then there is at least one point c ∈ (a, b) where f’(c) =0.

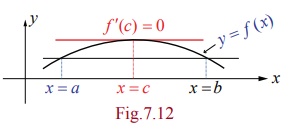
Geometrically this means that if the tangent is moving along the curve starting at x = a towards as in Fig 7.2 x = b then there exists a c ∈ ( a, b) at which the tangent is parallel to the x -axis.

Example 7.19

Compute the value of 'c ' satisfied by the Rolle’s theorem for the function

f(x) = x ² (1 − x)² , x ∈[0,1] .

Solution

Observe that, f(0) = 0 = f (1), f (x) is continuous in the interval [0,1] and is differentiable in (0,1) . Now,

f ′( x) = 2x (1− x)(1− 2x) .

Therefore, f ′(c) = 0 gives c = 0,1 , and 1/2

which ⇒ c = 1/2 ∈(0,1) .

Example 7.20

Find the value in the interval (1/2, 2) satisfied by the Rolle's theorem for the function f(x) = x + 1/x , x ∈ [1/2 , 2] .

Solution

We have, f (x) is continuous in [1/2 , 2] and differentiable in (1/2 , 2) with f(1/2) = 5/2 = f (2) . By the Rolle’s theorem there must exist a value c ∈ (1/2 , 2) such that,

 f (c) = 1 – 1/c² = 0 ⇒ c² = 1 gives c = ±1. As 1∈ (1/2 , 2) , we choose c = 1.

Example 7.21

Compute the value of 'c ' satisfied by Rolle’s theorem for the function 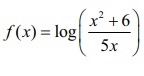 in the interval [2, 3].

Solution

Observe that, f(2) = 0 = f (3) and f ( x) is continuous in the interval [2, 3] and differentiable in (2, 3) . Now,

Observe that − √6 ∉(2, 3) and hence c = + √6 satisfies the Rolle’s theorem.

Rolle’s theorem can also be used to compute the number of roots of an algebraic equation in an interval without actually solving the equation.

Example 7.22

Without actually solving show that the equation x⁴ + 2x³ − 2 = 0 has only one real root in the interval (0,1) .

Solution

Let f(x)= x⁴ + 2x³ − 2. Then f (x) is continuous in [0,1] and differentiable in (0,1) . Now,

f ′( x) = 4x³ + 6x² . If f ′(x) = 0 then,

2x² (2x + 3) = 0 .

Therefore, x = 0,− 3/2 but 0, − 3/2 ∉(0,1) .

Thus, f’(x) > 0, ∀x ∈(0,1) .

Hence by the Rolle’s theorem there do not exist a , b ∈(0,1) such that, f (a) = 0 = f (b) . Therefore the equation f (x) = 0 cannot have two roots in the interval (0,1) . But, f (0) = −2 < 0 and f (1) = 1 > 0 tells us the curve y = f ( x) crosses the x -axis between 0 and 1 only once by the Intermediate value theorem. Therefore the equation x⁴ + 2x³ − 2 = 0 has only one real root in the interval (0,1) .

As an application of the Rolle’s theorem we have the following,

Example 7.23

Prove using the Rolle’s theorem that between any two distinct real zeros of the polynomial

a₀xⁿ + a_n-1x^n−1 + ….. + a₁x + a₀

there is a zero of the polynomial

na_nx^{n −1} + ( n −1)a_n−1x^n−2 + … + a₁.

Solution

Let P ( x) = a₀xⁿ + a_n-1x^n−1 + ….. + a₁x + a₀. Let α < β be two real zeros of P ( x) . Therefore, P (α ) = P(β ) = 0 . Since P ( x) is continuous in [α , β ] and differentiable in (α , β ) by an application of Rolle’s theorem there exists γ ∈ (α, β ) such that P (γ ) = 0. Since,

P′(x) = na_nx^{n −1} + ( n −1)a_n−1x^n−2 + … + a₁.

which completes the proof.

Example 7.24

Prove that there is a zero of the polynomial, 2x³ − 9x² −11x +12 in the interval (2, 7) given that and 7 are the zeros of the polynomial x⁴ − 6x³ −11x² + 24x + 28 .

Solution

Applying the above example 7.23 with

P(x) = x ⁴ − 6x³ − 11x² + 24x + 28, α = 2, β = 7

and observing

P’( x) / 2 = 2x³ − 9x² − 11x +12 = Q(x) , (say).

This implies that there is a zero of the polynomial Q ( x) in the interval (2, 7) .

For verification,

Q(2) = 16−36−22+12 = 28−58 =−30<0

Q(7) = 686 − 441− 77 +12 = 698 − 518 =180 > 0

From this we may see that there is a zero of the polynomial Q ( x) in the interval (2, 7) .

Remark

There are functions for which Rolle’s theorem may not be applicable.

(1) For the function f ( x) = | x |, x ∈[−1,1] Rolle’s theorem is not applicable, even though f (−1) = 1 = f (1) because f ( x) is not differentiable at x = 0 .

(2) For the function,

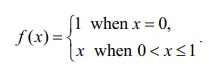
even though f (0) = f (1) = 1 , Rolle's theorem is not applicable because the function f ( x) is not continuous at x = 0 .

(3) For the function f (x) = sin x , x ∈ [0, π/2] Rolle’s theorem is not applicable, even though f (x) is continuous in the closed interval [0, π/2] and differentiable in the open interval (0, π/2) because, 0 = f (0) ≠ f(π/2) = 1.

If f ( x) is continuous in the closed interval [a , b] and differentiable in the open interval (a , b) and even if f ( a) ≠ f (b) then the Rolle’s theorem can be generalised as follows.

Theorem 7.1 (Intermediate value theorem)

If f is continuous on a closed interval [a , b] , and c is any number between f (a) and f (b) inclusive, then there is at least one number x in the closed interval [a , b] , such that f ( x) = c .