Differentials and Partial Derivatives

Differentials and Partial Derivatives

Introduction

Motivation

In real life we have to deal with many functions. Many times we have to estimate the change in the function due to change in the independent variable. Here are some real life situations.

• Suppose that a thin circular metal plate is heated uniformly. Then it’s radius increases and hence its area also increases. Suppose we can measure the approximate increase in the radius. How can we estimate the increase in the area of a circular plate?

• Suppose water is getting filled in water tank that is in the shape of an inverted right circular cone. In this process the height of the water level changes, the radius of the water level changes and the volume of the water in the tank changes as time changes. In a small interval of time, if we can measure the change in the height, change in the radius, how can we estimate the change in the volume of the water in the interval?

• A satellite is launched into the space from a launch pad. A camera is being set up, to observe the launch, at a safe distance from the launch pad. As the satellite lifts up, camera’s angle of elevation changes. If we know the two consecutive angles of elevation, within a small interval of time, how can we estimate the distance traveled by the satellite during that short interval of time?

To address these type of questions, we shall use the ideas of derivatives and partial derivatives to find linear approximations and differentials of the functions involved.

In the earlier chapters we have learnt the concept of derivative of a real-valued function of a single real variable. We have also learnt its applications in finding extremum of a function on its domain, and sketching the graph of a function. In this chapter, we shall see one more application of the derivative in estimating values of a function at some point. We know that linear functions, y = mx + b , are easy to work with; whereas nonlinear functions are computationally a bit tedious to work with.

For instance, if we have two functions, say f (x) = √( x +1), g(x ) = 2x − 7 and suppose that we want to evaluate these functions at say x = 3.25 . Which one will be easy to evaluate? Obviously, g(3.25) will be easier to calculate than f (3.25) . If we are ready to accept some error in calculating f (3.25) , then we can find a linear function that approximates f near x = 3 and use this linear function to obtain an approximate value of f (3.25) .We know that the graph of a function is a nonvertical line if and only if it is a linear function. Out of infinitely many straight lines passing through any given point on the graph of the function, only tangent line gives a good approximation to the function, because the graph of f looks approximately a straight line on the vicinity of the point (3,2).

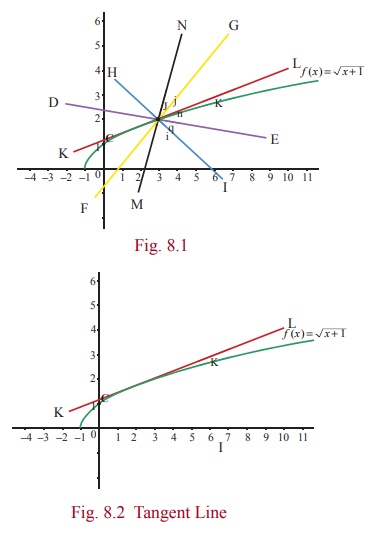
From the figures above it is clear that among these straight lines, only the tangent line to the graph of f ( x) at x = 3 gives a good approximation near the point x = 3 . Basically we are “linearizing” the given function at a selected point (3, 2) . This idea helps us in estimating the change in the function value near the chosen point through the change in the input. We shall use “derivative” to introduce the concept of “differential” which approximates the change in the function and will also be useful in calculating approximate values of a function near a chosen point. The derivative measures the instantaneous rate of change where as the differential approximates the change in the function values. Also, differentials are useful later in solving differential equations and evaluating definite integrals by the substitution method.

After learning differentials, we will focus on real valued functions of several variables. For functions of several variables, we shall introduce “partial derivatives”, a generalization of the concept of “derivative” of real-valued function of one variable. Why should we consider functions of more than one variable? Let us consider a simple situation that will explain the need. Suppose that a company is producing say pens and notebooks. This company is interested in maximizing its profit; then it has to find out the production level that will give maximum profit. To determine this, it has to analyze its revenue, cost, and profit functions, which are, in this case, functions of two variables (pen, notebook). Similarly, if we want to consider the volume of a box, then it will be a function of three variables namely length, width, and height. Also, the economy of a country depends on so many sectors and hence it depends on many variables. Thus it is necessary and important to consider functions involving more than one variable and develop the “concept of derivative” for functions of more than one variable. We shall also develop the concept of “differential” for functions of two and three variables and consider some of its applications. In this chapter, we shall consider only real-valued functions.

Learning Objectives

Upon completion of this chapter, students will be able to

• calculate the linear approximation of a function of one variable at a point

• approximate the value of a function using its linear approximation without calculators

• calculate the differential of a function

• apply linear approximation, differential in problems from real life situations

• find partial derivatives of a function of more than one variable

• calculate the linear approximation of a function of two or more variables

• determine if a given function of several variables is homogeneous or not

• apply Euler’s theorem for homogeneous functions.