Problem Questions with Answer, Solution - Exercise 8.2: Differentials | 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Chapter: 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Exercise 8.2: Differentials
EXERCISE 8.2
1. Find differential dy for each of the following functions :
(i) y = (1ŌłÆ2x)3 / 3ŌłÆ4x
(ii) y = (3 + sin(2x))2/3
(iii) y = ex2-5x+7 cos (x2-1)

2. Find df for f (x) = x2 + 3x and evaluate it for
(i) x = 2 and dx = 0.1
(ii) x = 3 and dx = 0.02

3. Find Δf and df for the function f for the indicated values of x , Δx and compare
(i) f (x) = x3 ŌłÆ 2x2 ; x = 2, ╬öx = dx = 0.5
(ii) f (x) = x2 + 2x + 3; x = ŌłÆ0.5, ╬öx = dx = 0.1
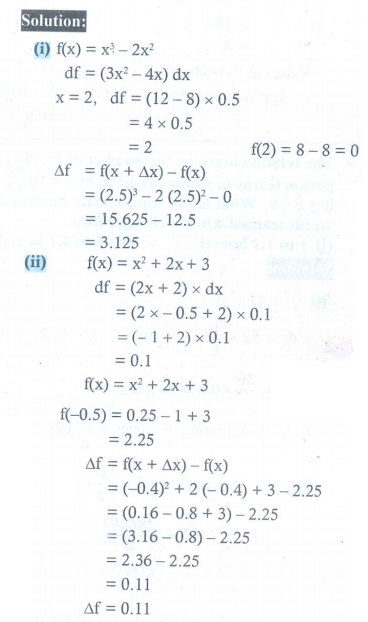
4. Assuming log10 e = 0.4343 , find an approximate value of log10 1003 .

5. The trunk of a tree has diameter 30 cm. During the following year, the circumference grew 6 cm.
(i) Approximately, how much did the treeŌĆÖs diameter grow?
(ii) What is the percentage increase in area of the treeŌĆÖs cross-section?

6. An egg of a particular bird is very nearly spherical. If the radius to the inside of the shell is 5 mm and radius to the outside of the shell is 5.3 mm, find the volume of the shell approximately.

7. Assume that the cross section of the artery of human is circular. A drug is given to a patient to dilate his arteries. If the radius of an artery is increased from 2 mm to 2.1 mm, how much is cross-sectional area increased approximately?

8. In a newly developed city, it is estimated that the voting population (in thousands) will increase according to V (t) = 30 +12t2 ŌłÆ t3 , 0 Ōēż t Ōēż 8 where t is the time in years. Find the approximate change in voters for the time change from 4 to 4 1/6 year.

9. The relation between the number of words y a person learns in x hours is given by y = 52ŌłÜx, 0 Ōēż x Ōēż 9 . What is the approximate number of words learned when x changes from
(i) 1 to 1.1 hour?
(ii) 4 to 4.1 hour?
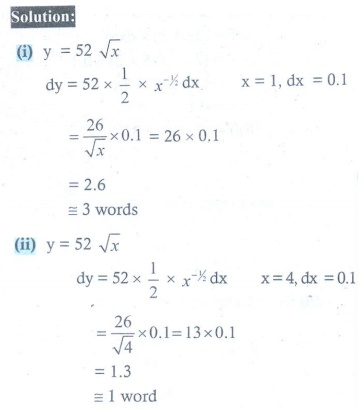
10. A circular plate expands uniformly under the influence of heat. If itŌĆÖs radius increases from 10.5 cm to 10.75 cm, then find an approximate change in the area and the approximate percentage change in the area.

11. A coat of paint of thickness 0.2 cm is applied to the faces of a cube whose edge is 10 cm. Use the differentials to find approximately how many cubic centimeters of paint is used to paint this cube. Also calculate the exact amount of paint used to paint this cube.

Answers:
1. 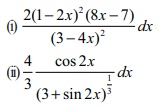
(iii) ex2ŌłÆ 5 x+7 [(2x ŌłÆ 5) cos(x2 ŌłÆ1) ŌłÆ 2x sin(x2 ŌłÆ1)] dx
2. (i) 0.7ŌĆā (ii) 0.18
3.ŌĆé (i) ╬öf = 3.125 , df = 2.0 (ii) ╬öf = 0.11, df = 0.1
4. 3.0013029ŌĆā
5. (i) 6/ŽĆ cm (ii) 40/ŽĆ %
6.ŌĆé 30ŽĆ mm3
7. 0.4ŽĆ mm2
8.ŌĆé 8000
9. (i) Ōēł 3 words (ii) Ōēł 1 word
10. 5.25ŽĆ , 4.76%
11.ŌĆé 60 cm3 , 61.2 cm3
Related Topics