Linear Approximation

Linear Approximation and Differentials

Linear Approximation

In this section, we introduce linear approximation of a function at a point. Using the linear approximation, we shall estimate the function value near a chosen point. Then we shall introduce differential of a real-valued function of one variable, which is also useful in applications.

Let f : (a, b) → ℝ be a differentiable function and x ∈(a, b) . Since f is differentiable at x , we have

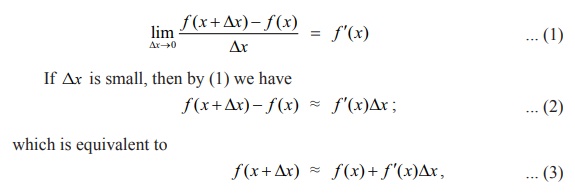
where ≈ means “approximately” equal. Also, observe that as the independent variable changes from x to x + xΔ, the function value changes from f ( x) to f ( x + Δx) . Hence if Δx is small and the change in the output is denoted by Δf or Δy , then (2) can be rewritten as

change in the output = Δy = Δf = f ( x + Δx) − f (x) ≈ f ‘(x) Δx.

Note that (3) helps in approximating the value of f ( x + Δx) using f ( x) and f ‘ ( x) Δx . Also, for a fixed x₀ , y( x ) = f ( x₀ ) + f ′( x₀ )( x − x₀ ), x ∈ R, gives the tangent line for the graph of f at ( x₀ , f ( x₀ )) which gives a good approximation to the function f near x₀ . This leads us to define

Definition 8.1 (Linear Approximation)

Let f : (a, b) → ℝ be a differentiable function and x₀ ∈(a, b) . We define the linear approximation L of f at x₀ by

L ( x) = f ( x₀ ) + f ′( x₀ )( x − x₀ ), ∀x ∈ (a, b)                 ... (4)

Note that by (3) and (4) we see that

f ( x + Δx) ≈ f (x) + f ′ (x) Δx ,

which is useful in approximating the value of f ( x + Δx).

Note that linear approximation for f at x₀ gives a good approximation to f ( x) if x is close to x₀ , because

Tangent line x = f (x₀) + f ′(x₀)(x−x₀)

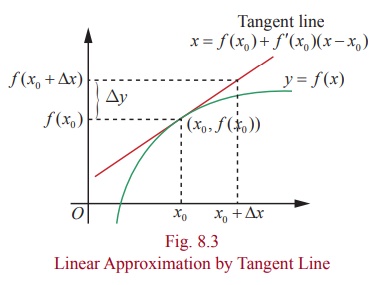
Error = f (x) − L ( x) = f (x ) − f (x₀ ) − f ′(x₀ )(x − x₀ )    ... (5)

approaches zero as x approaches to x₀ by continuity of f at x₀ . Also, if f ( x) = mx + c , then its linear approximation is L ( x) = (mx₀ + c ) + m(x − x₀ ) = mx + c = f (x) , for any point x ∈(a, b) . That is, the linear approximation, in this case, is the original function itself (is it not surprising?).

Example 8.1

Find the linear approximation for f (x) = √(1+x) , x ≥ −1, at x₀ = 3. Use the linear approximation to estimate f (3.2) .

Solution

We know from (4), that L(x) = f (x₀) + f ′(x₀)(x − x₀) . We have x₀ = 3, Δx = 0.2 and hence f (3) = √(1+ 3) = 2 . Also,

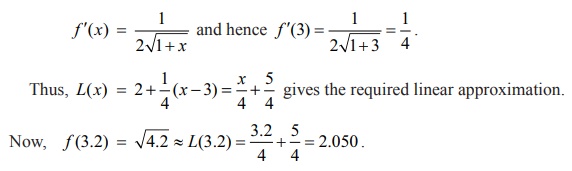
Actually, if we use a calculator to calculate we get √4.2 = 2.04939.