Partial Derivatives

Partial Derivatives

In this section, we shall see how the concept of derivative for functions of one variable may be generalized to real-valued function of several variables. First we consider functions of two variables.

Let A = { ( x, y ) | a < x < b, c < y < d } ⊂ ℝ² , and F : A → ℝ be a real-valued function. Suppose that (x₀ , y₀ ) ∈ A ; and we are interested in finding the rate of change of F at ( x₀ , y₀ ) with respect to the change only in the variable x . As we have seen above F ( x, y₀ ) is a function of x alone and it will represent a curve obtained by intersecting the surface z = F ( x , y) with y = y₀ plane. So we can discuss the slope of the tangent to the curve z = F ( x , y₀ ) at x = x₀ by finding derivative of F ( x, y₀ ) with respect to x and evaluating it at x = x₀ . Similarly, we can find the slope of the curve z = F ( x₀ , y) at y = y₀ by finding derivative of F ( x₀ , y) with respect to y and evaluating it at y = y₀ . These are the key ideas that motivate us to define partial derivatives below.

Definition 8.8

Let A = {( x, y )| a < x < b, c < y < d } ⊂ ℝ² , F : A → and ( x₀ , y₀ ) ∈ A

(i) We say that F has a partial derivative with respect to x at ( x₀ , y₀ ) ∈ A if

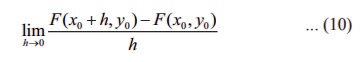
exists. In this case, the limit value is denoted by ∂F/∂x ( x₀ , y₀ ) .

(ii) We say F has a partial derivative with respect to y at ( x₀ , y₀ ) ∈ A if

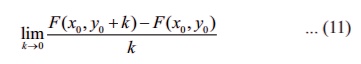
exists. In this case, the limit value is denoted by ∂F/∂y ( x₀ , y₀ ) .

Remarks

1. Partial derivatives for functions of three or more variables are defined exactly in a similar manner.

2. We read ∂F as “partial F ” and ∂x as “partial x ”. And we read ∂F/∂x as “partial F by partial x ”. It is also read as “dho F by dho x ”.

3. Similarly, we read ∂F/∂x as “partial F by partial y ” or as “dho F by dho y .

4. Sometimes ∂F/∂x ( x₀ , y₀ ) is also denoted by F_x( x₀ , y₀ ) or ∂F/∂x|_{( x0 , y0)}

Similarly ∂F/∂x Fy (x₀ , y₀ ) is denoted by F_y( x₀ , y₀ ) or ∂F/∂y|_{( x0 , y0)}

5. An important thing to notice is that while finding partial derivative of F with respect to x , we treat the y variable as a constant and find derivative with respect to x . That is, except for the variable with respect to which we find partial derivative, all other variables are treated as constants. That is why we call it as “partial derivative”.

6. If F has a partial derivative with respect to x at every point of A , then we say that ∂F/∂x ( x , y) exists on A . Note that in this case ∂F/∂x ( x , y) is again a real-valued function defined on A .

7. In the light of (4) , it is easy to see that all the rules (Sum, Product, Quotient, and Chain rules) of differentiation and formulae that we have learnt earlier hold true for the partial differentiation also.

Recall that for a function of one variable, differentiability at a point always implies continuity at that point. For a function F of two variables x , y we have defined ∂F/∂x (u , v) and ∂F/∂y (u , v) . Do the existence of partial derivatives of F at a point (u , v) implies continuity of F at (u , v) ? Following example illustrates that this may not necessarily happen always.

Example 8.11

Let f ( x , y) = 0 if xy ≠ 0 and f ( x , y) = 1 if xy = 0 .

(i) Calculate : ∂f /∂x ( 0, 0), ∂f /∂x(0, 0).

(ii) Show that f is not continuous at (0, 0) .

Solution

Note that the function f takes value 1 on the x , y -axes and 0 everywhere else on R² . So let us calculate

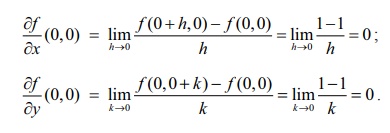
This completes (i).

Now for (ii) let us calculate the limit of f as ( x , y) → (0, 0) along the line y = x . Then lim_{( x , y ) →(0 , 0)} f (x , y) = 0 ; because along the line y = x when x ≠ 0, f ( x , y) = 0 , But f (0, 0) = 1 ≠ 0 ; hence f cannot be continuous at (0, 0).

Example 8.12

Let F ( x, y ) = x³y + y²x + 7 for all ( x , y) ∈ ℝ² . Calculate ∂F/∂x(−1, 3) and ∂F/∂x(−2,1) .

Solution

First we shall calculate ∂F/∂x(x, y), then we evaluate it at (−1, 3) . As we have already

observed, we find the derivative with respect to x holding y as a constant. That is,

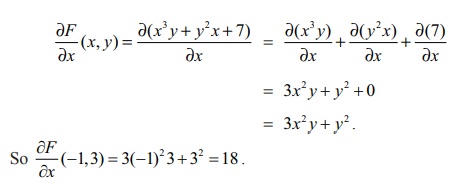
= 3x²y + y² + 0

= 3x²y + y².

So ∂F/∂x (−1, 3) = 3(−1)² 3 + 3² = 18 .

Next similarly we find partial derivative with respect to y.

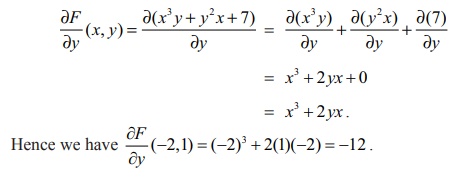
= x³ + 2 yx + 0 = x³ + 2 yx . Hence we have ∂F/∂x(−2,1) = (−2 )³ + 2(1)(−2 ) = −12 .

Note that in the above example ∂F/∂x(x , y) = 3x²y + y² , which is again a function of two variables. So we can take the partial derivative of this function with respect to x or y . For instance, if we take G ( x, y ) = 3x² y + y² , then we find ∂G/∂x = 6xy . Since G ( x , y) = ∂F/∂x , we have ∂G/∂x = ∂//∂x(∂F/∂x) = 6xy.

We denote this as ∂²F//∂²x ; which is called the second order partial derivative of F with respect to x.

Also, ∂G/∂y = 3x² + 2 y . Since G ( x , y) = ∂F/∂y , we have ∂G/∂y = ∂/∂y(∂F/∂y) = 3x² + 2y . We denote this as ∂²F / ∂y∂x ; which is called the mixed partial derivative of F with respect to x , y . Similarly we can also calculate ∂/∂x (∂F/∂y) = 3x² + 2y .

Also, if we differentiate ∂F / ∂y ( x , y) partially with respect to y we obtain ∂²F / ∂y²; which is called the second order partial derivatives of F with respect to y . So for any function F defined on any subset {(x,y) | a < x < b, c < y < d} ⊂ ℝ² we have the following notation :

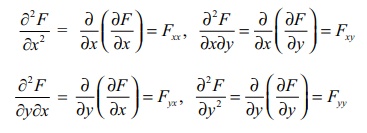
All the above are called second order partial derivatives of F . Similarly we can define higher order partial derivatives. For example,

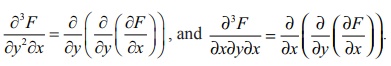
Next we shall see more examples on partial differentiation.

Example 8.13

Let f (x, y ) = sin(xy² ) + e^x3+5y for all ( x , y) ∈ ℝ² . Calculate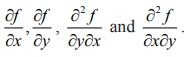 

Solution

Note that we have first used sum rule, then in the next step we have used chain rule. In the third step, product rule is used. Also, we see that f _xy = f _yx . Is it a coincidence? or is it always true? Actually, there are functions for which f _xy ≠ f _yx at some points. The following theorem gives conditions under which f _xy = f _yx .

Theorem 8.1 (Clairaut’s Theorem)

Suppose that A = {( x, y ) | a < x < b, c < y < d} ⊂ ℝ², F : A → ℝ. If f_xy and f _yx exist in A are continuous in A , then f _xy = f _yx in A .

We omit the discussion on the proof at this stage.

Definition 8.9

Let A = { ( x , y ) | a < x b, c < y < d } ⊂ ℝ². A function u : A → ℝ² is said to be harmonic in A if it satisfies ∂²u/∂²x + ∂²u/∂²y = 0, ∀(x , y) ∈ A . This equation is called Laplace’s equation.

Laplace’s equation occurs in the study of many natural phenomena like heat conduction, electrostatic field, fluid flows etc.

Example 8.15

Let u ( x, y ) = e^−2y cos(2x) for all ( x , y) ∈ ℝ² . Prove that u is a harmonic function in ℝ² .

Solution

We need to show that u satisfies the Laplace’s equation in ℝ² . Observe that u_x ( x, y ) = e^{−2 y} (−2) sin(2x) and hence u _xx (x, y ) = e^{−2 y} (−2)(2) cos(2x) .

Similarly, u _y (x, y ) = e^{−2 y} (−2) cos(2x) and u _yy (x, y ) = ( −2)(−2)e^{−2 y} cos(2x) .

Thus, u _xx + u_yy = −4 e ^{−2 y} cos(2x ) + 4e ^{−2 y} cos(2x) = 0.