Mathematics - Function of Function Rule | 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Chapter: 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Function of Function Rule
Function of
Function Rule
Let F be a function of two variables x , y.
Sometimes these variables may be functions of a single variable having same
domain. In this case, the function F
ultimately depends only on one variable. So we should be able to treat this F as a function of single variable and
study about dF/dt . In fact, this is
not a coincidence, it can be proved that
Theorem 8.2
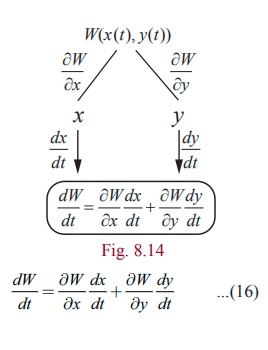
Suppose that W ( x, y)
is a function of two variables x , y having partial derivatives ŌłéW/Ōłéx , ŌłéW/Ōłéy . If both the variables x , y are differentiable functions of a single
variable t , then W is a differentiable function of t and
Let us
consider an example illustrating the above theorem.
Example 8.18
Verify
the above theorem for F ( x, y
) =
x2 ŌłÆ
2 y2 +
2xy and x (t) = cos t , y(t
) = sin t,
t Ōłł[0, 2ŽĆ ] .
Solution
Let F(x,y) = x2
ŌĆō 2y2 + 2xy and x(t) = cost, y(t) = sint.
Then F ( x,
y ) = cos2t ŌłÆ 2 sin2t
+
2 cos t sin t and thus F has becomes
a function of one
variable
t . So by using chain rule, we see
that
dF/dt = 2 cos t (ŌłÆ sin t) ŌłÆ 4
sin t cos t + 2(ŌłÆsin2 t + cos2 t)
= ŌłÆ6
cos t sin t + 2(ŌłÆ sin2 t + cos2 t) .
On the
other hand if we calculate
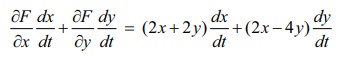
= 2(cos t
+
sin t)(ŌłÆsin t ) + 2(cos t ŌłÆ 2 sin t )(cos t)
= ŌłÆ6 cos t sin t + 2(ŌłÆ sin2 t + cos2 t)
= dF /dt
Example 8.19
Let g ( x,
y ) = x2
ŌłÆ
yx + sin(x + y), x (t)
=
e3t , y(t ) = t2
, t Ōłł ŌäØ. Find dg/dt.
Solution
We shall
follow the tree diagram to calculate.
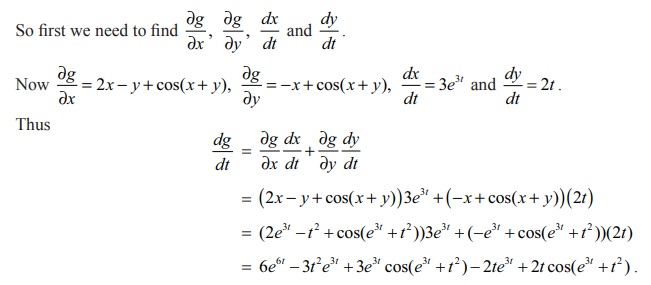
Also,
some times our W ( x, y)
will be such that x =
x(s
, t) , and y = y(s , t)
where s , t Ōłł ŌäØ. Then W can be considered as a function that depends on s and t . If x , y both have partial derivatives with
respect to s , t and W has partial
derivatives with respect to x and y , then we can calculate the partial
derivatives of W with respect to s and t using the following theorem.
Theorem 8.3
Suppose that W ( x, y)
is a function of two variables x , y having partial derivatives ŌłéW/Ōłéx , ŌłéW/Ōłéy . If both variables x = x(s,t) and y = y(s,t), where s , t Ōłł ŌäØ, have partial derivatives
with respect to both s and t, then
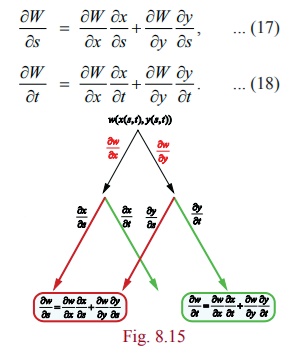
We omit
the proof. The above theorem is very useful. For instance, consider the
situation in which x = r cos╬Ė , and y = sin ╬Ė ,
r Ōēź 0 and ╬Ė Ōłł ŌäØ, (change from cartesian co-ordinate
to polar co-ordinate system). The
above theorem can be generalized for functions having n number of variables.
Let us
consider an example.
Example 8.20
Let g ( x,
y ) = 2 y + x 2 , x = 2r ŌłÆ s, y = r2
+
2s , r, s Ōłł
ŌäØ. Find
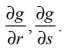
Solution
Here again we shall use the tree diagram to calculate
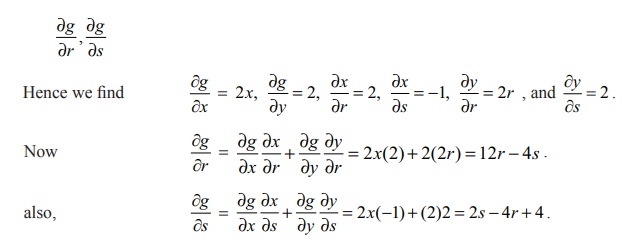
Related Topics