Problem Questions with Answer, Solution - Exercise 8.7: Homogeneous Functions and EulerŌĆÖs Theorem | 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Chapter: 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Exercise 8.7: Homogeneous Functions and EulerŌĆÖs Theorem
Maths Book back answers and solution for Exercise questions - Mathematics : Differentials and Partial Derivatives: Homogeneous Functions and EulerŌĆÖs Theorem - Exercise Problem Questions with Answer, Solution
EXERCISE 8.7
1. In each of the following cases, determine whether the following function is homogeneous or not. If it is so, find the degree.
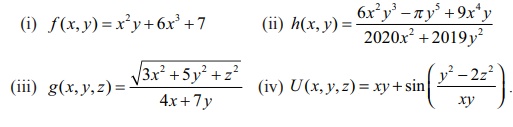

2. Prove that f (x, y) = x3 ŌłÆ 2x2y + 3xy2 + y3 is homogeneous; what is the degree? Verify EulerŌĆÖs Theorem for f .

3. Prove that g(x, y) = x log (y/x) is homogeneous; what is the degree? Verify EulerŌĆÖs Theorem for g.
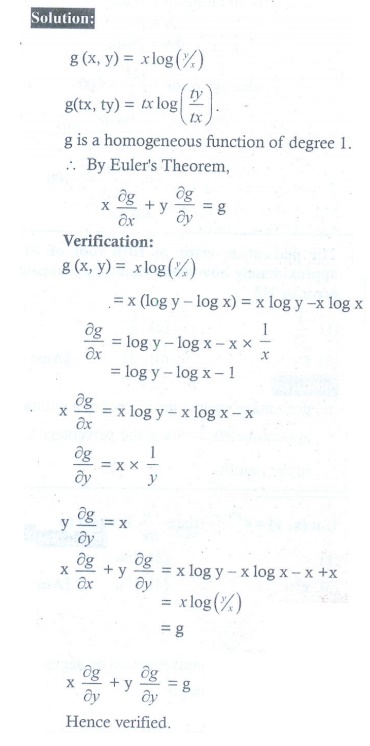
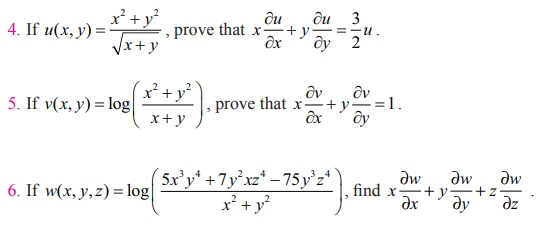



Answers:
1. (i) not homogeneous (ii) Homogeneous, deg.3 (iii) homogeneous, deg.0 (iv) not homogeneous
6. 5
Tags : Problem Questions with Answer, Solution , 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
12th Maths : UNIT 8 : Differentials and Partial Derivatives : Exercise 8.7: Homogeneous Functions and EulerŌĆÖs Theorem | Problem Questions with Answer, Solution
Related Topics
12th Maths : UNIT 8 : Differentials and Partial Derivatives