Errors: Absolute Error, Relative Error, and Percentage Error

Errors: Absolute Error, Relative Error, and Percentage Error

When we are approximating a value, there occurs an error. In this section, we consider the error, which occurs by linear approximation, given by (4). We shall consider different types of errors. Taking h = x − x₀ , we get x = x₀ + h , then (5) becomes

E ( h) = f (x₀ + h ) − f (x₀ ) − f ′(x₀ )h .          ... (6)

Note that E(0) = 0 and as we have already observed lim_h→0 E ( h) = 0 follows from the continuity of f at x₀ . In addition, if f is differentiable, then from (1), it follows that

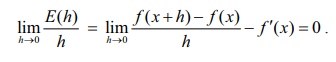
Thus when f is differentiable at x₀ , then the above equation shows that E ( h) actually approaches zero faster than h approaching zero. Now, we define

Definition 8.2

Suppose that certain quantity is to be determined. It’s exact value is called the actual value. Some times we obtain its approximate value through some approximation process. In this case, we define

Absolute error = Actual value − Approximate value.

So (6) gives the absolute error that occurs by a linear approximation. Let us look at an example illustrating the use of linear approximation.

Example 8.2

Use linear approximation to find an approximate value of √9.2 without using a calculator.

Solution

We need to find an approximate value of √9.2 using linear approximation. Now by (3), we have f (x₀ + Δx ) ≈ f (x₀ ) + f ′(x₀ ) Δx . To do this, we have to identify an appropriate function f , a point x₀ and Δx . Our choice should be such that the right side of the above approximate equality, should be computable without the help of a calculator. So, we choose f (x) = √x , x₀ = 9 and Δx = 0.2 . Then, f ′(x₀) = 1/2√9 and hence

√9.2 ≈ f (9) + f ′(9)(0.2) = 3 + 0.2/6 = 3.03333 .

Now if we use a calculator, just to compare, we find √9.2 = 3.03315 . We see that our approximation is accurate to three decimal places and the error is 3.03315 − 3.03333 = −0.00018 . [Also note that one could choose f (x) = √(1+ x) , x₀ = 8 and Δx = 0.2 . So the choice of f and x₀ are not necessarily unique].

So in the above example, the absolute error is 3. 03315 3.03333 0.00018 . Note that the absolute error says how much the error; but it does not say how good the approximation is. For instance, let us consider two simple cases.

Case 1 : Suppose that the actual value of something is 5 and its approximated value is 4 , then the absolute error is 5 − 4 = 1 .

Case 2 : Suppose that the actual value of something is 100 and its approximated value is 95. In this case, the absolute error is 100 − 95 = 5 . So the absolute error in the first case is smaller when compared to the second case.

Among these two approximations, which is a better approximation; and why? The absolute error does not give a clear picture about whether an approximation is a good one or not. On the other hand, if we calculate relative error or percentage of error (defined below), it will be easy to see how good an approximation is. If the actual value is zero, then we do know how close our approximate answer is to the actual value. So if the actual value is not zero, then we define,

Definition 8.3

If the actual value is not zero, then

Relative error = [ Actual value − Approximate value ] / Actual value

Percentage error = Relative error ×100 .

Note: Absolute error has unit of measurement where as relative error and percentage error are units free.

Note that, in the case of the above examples,

In the first case

The relative error = 1/5 = 0.2 ; and the percentage error = 1/5 ×100 = 20% .

In the second case

The relative error = 5/100 ; and the percentage error = 5/100 ×100 = 5%.

So the second approximation is a better approximation than the first one. Note that, in order to calculate the relative error or the percentage error one should know the actual value of what we are approximating.

Let us consider some examples.

Example 8.3

Let us assume that the shape of a soap bubble is a sphere. Use linear approximation to approximate the increase in the surface area of a soap bubble as its radius increases from 5 cm to 5.2 cm. Also, calculate the percentage error.

Solution

Recall that surface area of a sphere with radius r is given by S ( r) = 4Ï€ r² . Note that even though we can calculate the exact change using this formula, we shall try to approximate the change using the linear approximation. So, using (4), we have

Change in the surface area = S (5.2) − S(5) ≈ S′(5)(0.2)

= 8Ï€(5)( 0 .2) = 8Ï€ cm²

Exact calculation of the change in the surface gives

S (5.2) − S(5) = 108.16Ï€ - 100 Ï€ = 8.16 cm² .

Percentage error = relative error × 100 = { 8.16π−8Ï€ / 8.16Ï€  } × 100 = 1.9607%

Example 8.4

A right circular cylinder has radius r = 10 cm. and height h = 20 cm. Suppose that the radius of the cylinder is increased from 10 cm to 10.1 cm and the height does not change. Estimate the change in the volume of the cylinder. Also, calculate the relative error and percentage error.

Solution

Recall that volume of a right circular cylinder is given by V = Ï€ r²h , where r is the radius and h is the height. So we have V ( r) = Ï€r²h = 20Ï€r².

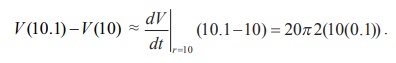
Thus the estimate for the change in the volume is 40Ï€ cm³.

Exact calculation of the volume change gives

V (10.1) −V (10) = 2040.2Ï€ − 2000Ï€ = 40.2Ï€ cm³.

So relative error = (40.2π−40Ï€) / (40.2Ï€)  = 1 / 201 = 0.00497 ; and hence

the percentage error = relative error × 100 = [1/201] × 100 = 0.497% .