Mathematics - Differentials | 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Chapter: 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Differentials
Differentials
Here
again, we use the derivative concept to introduce ŌĆ£DifferentialŌĆØ. Let us take
another look at (1),

Here df/dx is a notation, used by Leibniz, for
the limit of the difference quotient, which is called the differential coefficient of y with respect to x .Will it be meaningful to treat df/dx as a quotient of df and dx ? In other words, is it possible to assign meaning to df and dx so that derivative is equal to the quotient of df and dx .Well, in some cases yes. For instance, if f ( x) =
mx + c
, m, c are constants, then, y = f (
x) .
Δy = f ( x +
╬öx ) ŌłÆ f (x) = m╬öx = f ŌĆ▓(x)╬öx for all x Ōłł
ŌäØ and ╬öx
and
hence equality in both (2), and (3). In this case changes in x and y (= f ) are taking place along straight
lines, in which case we have,
change
in f / change in x =
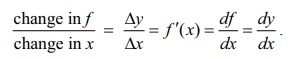
Thus in
this case the derivative df/dx is
truly a quotient of df and dx, if we take df = Δf = dy and dx = Δx. This leads us to define the
differential of f as follows:
Definition 8.4
Let f : (a,
b) ŌåÆ ŌäØ be a differentiable function, for x Ōłł(a, b) and ╬öx the increment given to x , we define the differential of f by
df = f ŌĆ▓
(x)Δx . ... (8)
First we
note that if f (x) = x , then by (8) we get dx = f
ŌĆ▓(x)╬ö x = 1╬öx which means that
the differential dx = Δx
, which is the change in x -axis.
So the differential given by (8) is same as df
= f ŌĆ▓(x)dx .

Linear Approximation and Differential
Next we explore
the differential for an arbitrary differentiable function y = f (x).
Then ╬öf = f ( x + dx ) ŌłÆ f (x) gives the change in output along the graph of y = f (x) and f ŌĆ▓(x) gives the slope of the tangent line at ( x , f (x)) . Let dy or df denote the increment in f along the tangent line. Then by the above observation, we have dy = f ŌĆ▓(x)dx .
From the
figure it is clear that ╬öf Ōēł dy = df
= f ŌĆ▓(x)dx and hence f ŌĆ▓ (x) can be viewed approximately as the
quotient of Δf and Δx. So we may interpret df/dx as the quotient of df and dx .
Remark
We know
that derivative of a function is again a function. On the other hand, differential
df of a function f is not only a function of the independent variable but also
depends on the change in the input namely dx
=
╬öx . So df is a function of two changing quantities namely x and dx. Observe that ╬öfŌēł df , which can be observed from the
Fig. 8.4.
In the
table below we give some functions, their derivatives and their differentials
side by side for comparative purpose.

Next we
look at the properties of differentials. These results easily follow from the
definition of differential and the rules for differentiation. We give a proof
for (5) below and the other proofs are left as exercises.
Properties of Differentials
Here we
consider real-valued functions of real variable.
(1) If f is a constant function, then df = 0 .
(2) If f (x) = x identity function, then df
= 1dx .
(3) If f is differentiable and c Ōłł R, then d(cf) = cf ŌĆ▓(x)dx .
(4) If f ,
g are differentiable, then d ( f +
g) = df + dg = f ŌĆ▓ (x)dx + gŌĆ▓(x)dx .
(5) If f ,
g are differentiable, then d ( fg ) = fdg + gdf = ( f (x) g ŌĆ▓ (
x) + f ŌĆ▓ (x) g ( x))dx.
(6) If f ,
g are differentiable, then 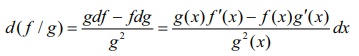 , where g(x)ŌēĀ0.
, where g(x)ŌēĀ0.
(7) If f ,
g are differentiable and h = f o g is
defined, then dh = f ŌĆ▓( g( x )) gŌĆ▓( x ) dx .
(8) If
h(x) = ef (x) , then dh = ef
(x) f ŌĆ▓( x ) dx .
(9) If f (x) > 0 for all x and g (x) = log( f (x)) , then dg = f ŌĆ▓(x)/f(x) dx .
Example 8.5
Let f ,
g : (a , b) ŌåÆ ŌäØ
be differentiable functions. Show that d(fg
) = fdg + gdf .
Solution
Let f ,
g : (a , b) ŌåÆ ŌäØ
be differentiable functions and h(x) = f
(x) g (x) . Then h , being a product of differentiable functions, is
differentiable on (a, b) . So by
definition dh = hŌĆ▓ ( x)dx. Now by using product rule we have hŌĆ▓ (x)
= f (x) gŌĆ▓ ( x) + f ŌĆ▓(x) g(x) .
Thus dh = hŌĆ▓
(x)dx = ( f (x) gŌĆ▓ ( x) + f ŌĆ▓ (x) g( x))dx = f
(x) gŌĆ▓ ( x)dx + f ŌĆ▓ (x) g( x)dx
= f (x)dg + g ( x)df = fdg + gdf
Example 8.6
Let g ( x)
=
x2 +
sin x . Calculate the differential dg .
Solution
Note
that g is differentiable and g ŌĆ▓(x)
=
2x + cos x .
Thus dg = (2x + cos x)dx .
Example 8.7
If the
radius of a sphere, with radius 10 cm, has to decrease by 0.1 cm, approximately
how much will its volume decrease?
Solution
We know
that volume of a sphere is given by V
=
4/3 ŽĆr3 , where r > 0 is the radius. So the differential
dV = 4ŽĆr2dr and hence
╬öV Ōēł dV
= 4ŽĆ(10)2 (9.9-10) cm3
= 4![]() 102 ( 0.1) cm3
102 ( 0.1) cm3
= ŌłÆ 40ŽĆ cm3.
Note
that we have used dr =
(9.9 ŌłÆ10)
cm, because radius decreases from 10 to 9.9. Again the negative sign in the
answer indicates that the volume of the sphere decreases about 40ŽĆ cm3.
Related Topics