Summary

SUMMARY

• Let f : (a, b) → ℝ be a differentiable function and x₀ ∈ (a, b) then linear approximation L of f at x₀ is given by

L(x) = f (x₀) + f  ′ (x₀) (x - x₀)  ∀ x ∈ (a,b)

• Absolute error = Actual value – Approximate value

Relative error = Absolute error / Actual value

Percentage error = Relative error × 100

(or)

Acutal value / Absolute error × 100

• Let f : ( a , b)→ ℝ be a differentiable function. For x ∈ ( a,b) and Δx the increment given to x, the differential of f is defined by df = f ′( x ) Δx .

• All the rules for limits (limit theorems) for functions of one variable also hold true for

functions of several variables.

• Let A = {( x , y ) | a < x < b, c < y < d }⊂ ℝ² , F : A → ℝ and ( x₀ , y₀ ) ∈ A .

• (i) F has a partial derivative with respect to x at ( x₀ , y₀ )∈ A

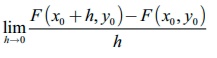
exists and it is denoted by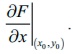 

F has a partial derivative with respect to y at ( x₀ , y₀ )∈ A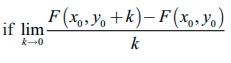 

exists and limit value is defined by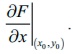 

• Clariant’s Theorem: Suppose that A = {( x , y ) a < x < b, c < y < d}⊂ ℝ² , F : A → ℝ . If f_xy and f _yx exist in A and are continuous in A, then f _xy = f_yx in A.

• Let A = {( x , y ) | a < x < b, c < y < d} ⊂ ℝ². A function U : A → ℝ is said to be harmonic in A if it satisfies ∂²u/∂x² + ∂²u/∂y² = 0, ∀( x , y)∈ A . This equation is called Laplace’s equation.

• Let A = {( x , y ) | a < x < b, c < y < d}⊂ ℝ² , F : A → ℝ and ( x₀ , y₀ )∈ A .

(i) The linear approximation of F at ( x₀ , y₀ )∈ A is defined to be

(ii) The differential of F is defined to be dF = ∂F/∂x dx + ∂F/∂y dy where Δx = dx and Δy = dy .

• Suppose w is a function of two variables x, y where x and y are functions of a single variable ‘t’ then  dw/dt = ∂w/∂x ⋅ dxdt + ∂w/∂y ⋅ dy/dt

• Suppose w is a function of two variables x and y where x and y are functions of two variables s and t then,

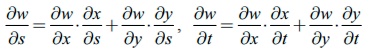
• Suppose that A = {( x , y ) | a < x < b, c < y < d}⊂ ℝ² , F : A → ℝ² . If F is having continuous partial derivatives and homogeneous on A, with degree p, then x ∂F/∂x + y ∂F/∂y = pF.