Exercise 8.4: Partial Derivatives

EXERCISE 8.4

1. Find the partial derivatives of the following functions at the indicated points.

(i) f (x, y ) = 3x2 − 2xy + y2 + 5x + 2,       (2, −5)

(ii) g( x, y ) = 3x2 + y2 + 5x + 2,         (1, −2)

(iii) h(x,y,z) = x sin(xy) + z2x       ( 2,π/4,1)

(iv) G ( x, y ) = ex+3y log(x2 + y2 ), (−1,1)

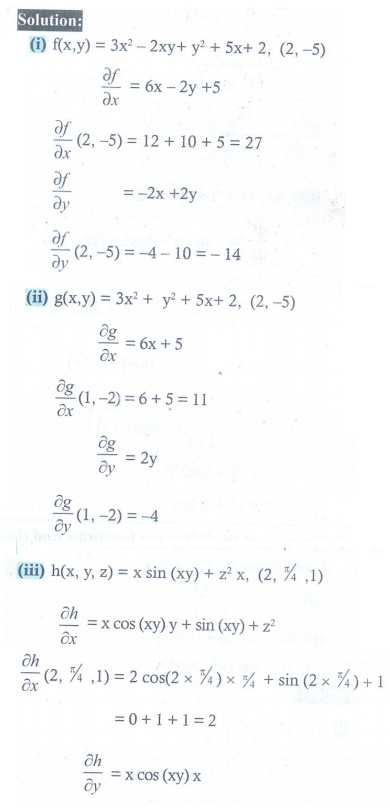
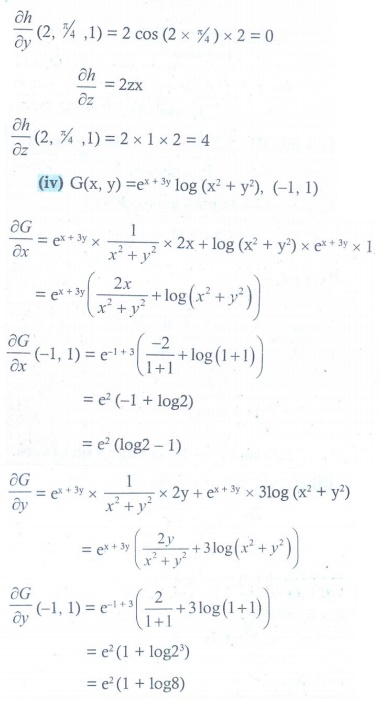
2. For each of the following functions find the fx , fy , and show that fxy = fyx.

(i) f (x , y) = 3x / y+sinx

(ii) f (x , y) = tan−1 (x/ y)

(iii) f (x, y ) = cos(x2 − 3xy)

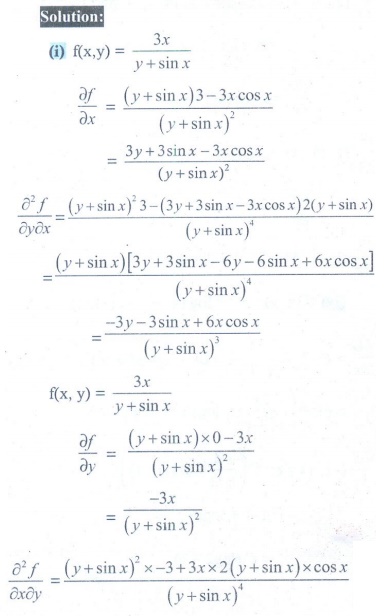
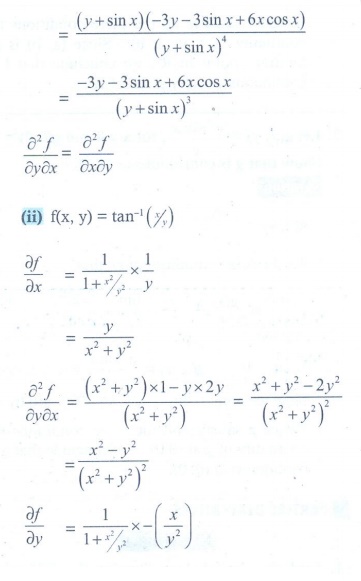
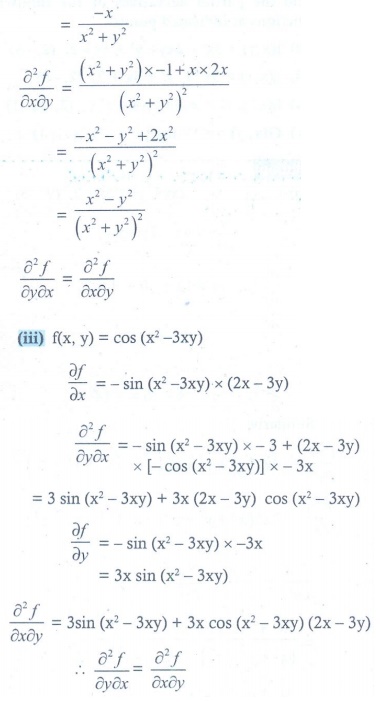
3. 

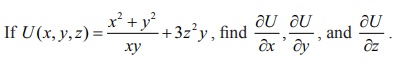
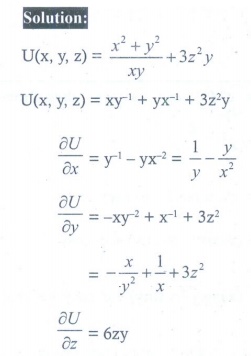
4. If U ( x, y , z) = log(x3 + y3 + z3 ) , find ∂U/∂x , ∂U/∂y , and ∂U/∂z .

5. For each of the following functions find the gxy , gxx , gyy and gyx.

(i) g ( x, y ) = xey + 3x2y

(ii) g ( x, y ) = log(5x + 3y)

(iii) g ( x, y ) = x2 + 3xy − 7y + cos(5x)

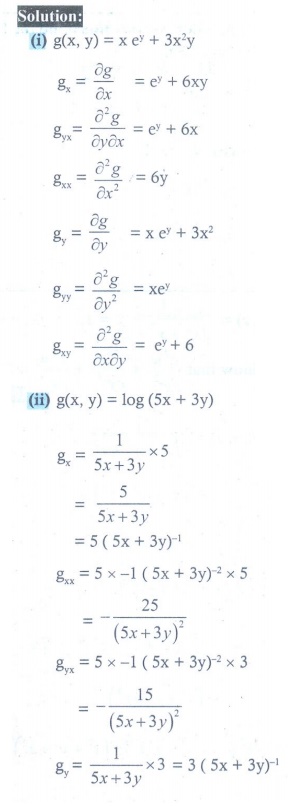
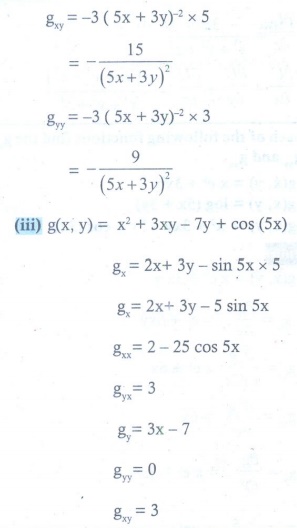
6. Let w( x, y , z) = 1 / √[x2 + y2 + z2] , (x , y, z) ≠ (0, 0, 0) . Show that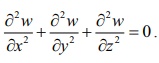 

7. If V ( x, y ) = ex(x cos y − y sin y) , then prove that ∂2V/∂x2 + ∂2V/∂y2= 0 .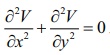

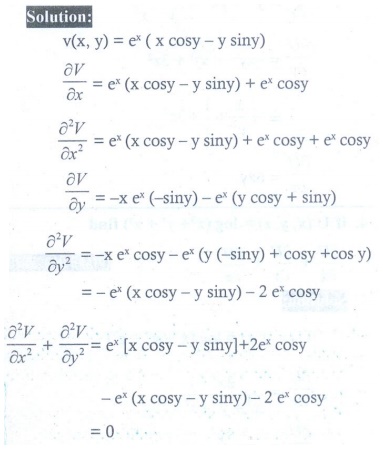
8. If w( x, y ) = xy + sin( xy) , then prove that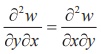 

9. If v ( x, y , z) = x3 + y3 + z3 + 3xyz , show that ∂2v / ∂y∂z  = ∂2v / ∂z∂y.

10. A firm produces two types of calculators each week, x number of type A and y number of type B . The weekly revenue and cost functions (in rupees) are ℝ ( x, y ) = 80x + 90 y + 0.04xy − 0.05x2 − 0.05 y2 and C ( x, y ) = 8x + 6 y + 2000 respectively.

(i) Find the profit function P ( x, y) ,

(ii) Find ∂P/∂x (1200,1800) and ∂p/∂y (1200,1800) and interpret these results.

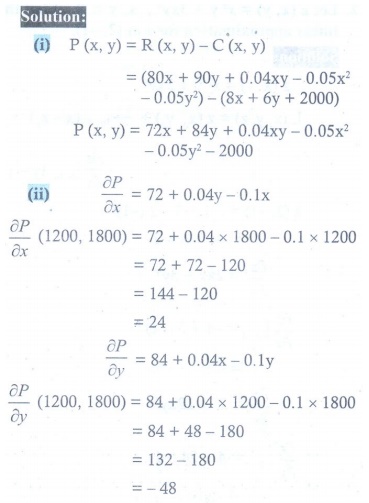
Answers:

1. (i) 27, − 14 (ii) 11, −4 (iii) 2, 0, 4 (iv) e2((log 2)) − 1), e2(1+log 8)

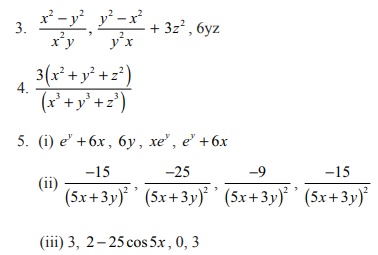
10. (i) 72x + 84 y + 0.04xy − 0.05x2 − 0.05 y2 − 2000 (ii) 24, −48 , Keeping y constant and increasing x increases profit.